4. Functions

4.1. Functions

In Python, a function is a named sequence of statements that belong together. Their primary purpose is to help us organize programs into chunks that match how we think about the problem.

The syntax for a function definition is:

def <NAME>( <PARAMETERS> ):
    <STATEMENTS>

We can make up any names we want for the functions we create, except that we can’t use a name that is a Python keyword, and the names must follow the rules for legal identifiers.

There can be any number of statements inside the function, but they have to be indented from the def. In the examples in this book, we will use the standard indentation of four spaces. Function definitions are the second of several compound statements we will see, all of which have the same pattern:

1. A header line which begins with a keyword and ends with a colon.
2. A body consisting of one or more Python statements, each indented the same amount — the Python style guide recommends 4 spaces — from the header line.

We’ve already seen the for loop which follows this pattern.

So looking again at the function definition, the keyword in the header is def, which is followed by the name of the function and some parameters enclosed in parentheses. The parameter list may be empty, or it may contain any number of parameters separated from one another by commas. In either case, the parentheses are required. The parameters specifies what information, if any, we have to provide in order to use the new function.

Suppose we’re working with turtles, and a common operation we need is to draw squares. “Draw a square” is an abstraction, or a mental chunk, of a number of smaller steps. So let’s write a function to capture the pattern of this “building block”:

 import turtle

 def draw_square(animal, size):
     """
     Make animal draw a square with sides of length size.
     """
     for _ in range(4):
         animal.forward(size)
         animal.left(90)


 window = turtle.Screen()        # Set up the window and its attributes
 window.bgcolor("lightgreen")
 window.title("Alex meets a function")

 alex = turtle.Turtle()      # Create alex
 draw_square(alex, 50)       # Call the function to draw the square
 window.mainloop()

This function is named draw_square. It has two parameters: one to tell the function which turtle to move around, and the other to tell it the size of the square we want drawn. Make sure you know where the body of the function ends — it depends on the indentation, and the blank lines don’t count for this purpose!

Docstrings for documentation

If the first thing after the function header is a string, it is treated as a docstring and gets special treatment in Python and in some programming tools.

Docstrings are the key way to document our functions in Python and the documentation part is important. Because whoever calls our function shouldn’t have to need to know what is going on in the function or how it works; they just need to know what arguments our function takes, what it does, and what the expected result is. Enough to be able to use the function without having to look underneath. This goes back to the concept of abstraction of which we’ll talk more about.

Docstrings are usually formed using triple-quoted strings as they allow us to easily expand the docstring later on should we want to write more than a one-liner.

Just to differentiate from comments, a string at the start of a function (a docstring) is retrievable by Python tools at runtime. By contrast, comments are completely eliminated when the program is parsed.

Defining the function just tells Python how to do a particular task, not to perform it. In order to execute a function we need to make a function call. We’ve already seen how to call some built-in functions like print, range and int. Function calls contain the name of the function being executed followed by a list of values, called arguments, which are assigned to the parameters in the function definition. So in the second last line of the program, we call the function, and pass alex as the turtle to be manipulated, and 50 as the size of the square we want. While the function is executing, then, the variable size refers to the value 50, and the variable animal refers to the same turtle instance that the variable alex refers to. We called it animal to signify that there is no meaning to the name you give a function argument.

Once we’ve defined a function, we can call it as often as we like, and its statements will be executed each time we call it. And we could use it to get any of our turtles to draw a square. In the next example, we’ve changed the draw_square function a little, and we get tess to draw 15 squares, with some variations.

import turtle

def draw_multicolor_square(animal, size):
    """Make animal draw a multi-color square of given size."""
    for color in ["red", "purple", "hotpink", "blue"]:
        animal.color(color)
        animal.forward(size)
        animal.left(90)

window = turtle.Screen()        # Set up the window and its attributes
window.bgcolor("lightgreen")

tess = turtle.Turtle()      # Create tess and set some attributes
tess.pensize(3)

size = 20                   # Size of the smallest square
for _ in range(15):
    draw_multicolor_square(tess, size)
    size += 10              # Increase the size for next time
    tess.forward(10)        # Move tess along a little
    tess.right(18)          #    and give her some turn

window.mainloop()

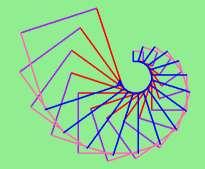
4.2. Functions can call other functions

Let’s assume now we want a function to draw a rectangle. We need to be able to call the function with different arguments for width and height. And, unlike the case of the square, we cannot repeat the same thing 4 times, because the four sides are not equal.

So we eventually come up with this rather nice code that can draw a rectangle.

def draw_rectangle(animal, width, height):
    """Get animal to draw a rectangle of given width and height."""
    for _ in range(2):
        animal.forward(width)
        animal.left(90)
        animal.forward(height)
        animal.left(90)

Thinking like a scientist involves looking for patterns and relationships. In the code above, we’ve done that to some extent. We did not just draw four sides. Instead, we spotted that we could draw the rectangle as two halves, and used a loop to repeat that pattern twice.

But now we might spot that a square is a special kind of rectangle. We already have a function that draws a rectangle, so we can use that to draw our square.

def draw_square(animal, size):        # A new version of draw_square
    draw_rectangle(animal, size, size)

There are some points worth noting here:

• Functions can call other functions.
• Rewriting draw_square like this captures the relationship that we’ve spotted between squares and rectangles.
• A caller of this function might say draw_square(tess, 50). The parameters of this function, animal and size, are assigned the values of the tess object, and the int 50 respectively.
• In the body of the function they are just like any other variable.
• When the call is made to draw_rectangle, the values in variables animal and size are fetched first, then the call happens. So as we enter the top of function draw_rectangle, its variable animal is assigned the tess object, and width and height in that function are both given the value 50.

So far, it may not be clear why it is worth the trouble to create all of these new functions. Actually, there are a lot of reasons, but this example demonstrates two:

1. Creating a new function gives us an opportunity to name a group of statements. Functions can simplify a program by hiding a complex computation behind a single command. The function (including its name) can capture our mental chunking, or abstraction, of the problem.
2. Creating a new function can make a program smaller by eliminating repetitive code.

As we might expect, we have to create a function before we can execute it. In other words, the function definition has to be executed before the function is called.

4.3. Flow of execution

In order to ensure that a function is defined before its first use, we have to know the order in which statements are executed, which is called the flow of execution.

Execution always begins at the first statement of the program. Statements are executed one at a time, in order from top to bottom.

Function definitions do not alter the flow of execution of the program, but remember that statements inside the function are not executed until the function is called. Although it is not common, we can define one function inside another. In this case, the inner definition isn’t executed until the outer function is called.

Function calls are like a detour in the flow of execution. Instead of going to the next statement, the flow jumps to the first line of the called function, executes all the statements there, and then comes back to pick up where it left off.

That sounds simple enough, until we remember that one function can call another. While in the middle of one function, the program might have to execute the statements in another function. But while executing that new function, the program might have to execute yet another function!

Fortunately, Python is adept at keeping track of where it is, so each time a function completes, the program picks up where it left off in the function that called it. When it gets to the end of the program, it terminates.

What’s the moral of this sordid tale? When we read a program, don’t read from top to bottom. Instead, follow the flow of execution.

As a simple example, let’s consider the following program:

import turtle

def draw_square(animal, size):
    for _ in range(4):
        animal.forward(size)
        animal.left(90)

window = turtle.Screen()        # Set up the window and its attributes

tess = turtle.Turtle()      # Create tess and set some attributes

draw_square(tess, 50)

window.mainloop()

The Python interpreter reads this script line by line. At the first line the turtle module is imported. We then define draw_square, which contains the instructions for a given turtle to draw a square. However, nothing happens yet. We then go on to define a window, and our charming turtle tess. The next line calls ``draw_square, asking tess to draw a square with sides of length 50. Finally, window.mainloop() actually runs these executions, and you will see tess draw a square on the screen.

Being able to trace your program is a valuable skill for a programmer.

4.4. Functions that require arguments

Most functions require arguments: the arguments provide for generalization. For example, if we want to find the absolute value of a number, we have to indicate what the number is. Python has a built-in function for computing the absolute value:

>>> abs(5)
5
>>> abs(-5)
5

In this example, the arguments to the abs function are 5 and -5.

Some functions take more than one argument. For example the built-in function pow takes two arguments, the base and the exponent. Inside the function, the values that are passed get assigned to variables called parameters.

>>> pow(2, 3)
8
>>> pow(7, 4)
2401

Another built-in function that takes more than one argument is max.

>>> max(7, 11)
11
>>> max(4, 1, 17, 2, 12)
17
>>> max(3 * 11, 5**3, 512 - 9, 1024**0)
503

max can be passed any number of arguments, separated by commas, and will return the largest value passed. The arguments can be either simple values or expressions. In the last example, 503 is returned, since it is larger than 33, 125, and 1.

4.5. Functions that return values

All the functions in the previous section return values. Calling each of these functions generates a value, which we usually assign to a variable or use as part of an expression.

biggest = max(3, 7, 2, 5)
x = abs(3 - 11) + 10

So an important difference between these functions and one like draw_square is that draw_square was not executed because we wanted it to compute a value — on the contrary, we wrote draw_square because we wanted it to execute a sequence of steps that caused the turtle to draw.

A function that returns a value is called a fruitful function in this book. The opposite of a fruitful function is void function — one that is not executed for its resulting value, but is executed because it does something useful. (Languages like Java, C#, C and C++ use the term “void function”, other languages like Pascal call it a procedure.) Even though void functions are not executed for their resulting value, Python always wants to return something. So if the programmer doesn’t arrange to return a value, Python will automatically return the value None.

How do we write our own fruitful function? In the exercises at the end of chapter 2 we saw the standard formula for compound interest, which we’ll now write as a fruitful function:

def final_amount(p, r, n, t):
    """
      Apply the compound interest formula to p
       to produce the final amount.
    """

    a = p * (1 + r/n) ** (n*t)
    return a         # This is new, and makes the function fruitful.

# now that we have the function above, let us call it.
toInvest = float(input("How much do you want to invest?"))
fnl = final_amount(toInvest, 0.08, 12, 5)
print("At the end of the period you'll have", fnl)

• The return statement is followed an expression (a in this case). This expression will be evaluated and returned to the caller as the “fruit” of calling this function.

• We prompted the user for the principal amount. The type of toInvest is a string, but we need a number before we can work with it. Because it is money, and could have decimal places, we’ve used the float type converter function to parse the string and return a float.

• Notice how we entered the arguments for 8% interest, compounded 12 times per year, for 5 years.

• When we run this, we get the output

  At the end of the period you’ll have 14898.457083

  This is a bit messy with all these decimal places, but remember that Python doesn’t understand that we’re working with money: it just does the calculation to the best of its ability, without rounding. Later we’ll see how to format the string that is printed in such a way that it does get nicely rounded to two decimal places before printing.

• The line toInvest = float(input("How much do you want to invest?")) also shows yet another example of composition — we can call a function like float, and its arguments can be the results of other function calls (like input) that we’ve called along the way.

Notice something else very important here. The name of the variable we pass as an argument — toInvest — has nothing to do with the name of the parameter — p. It is as if p = toInvest is executed when final_amount is called. It doesn’t matter what the value was named in the caller, in final_amount its name is p.

These short variable names are getting quite tricky, so perhaps we’d prefer one of these versions instead:

def final_amount_v2(principal_amount, nominal_percentage_rate,
                                    num_times_per_year, years):
    a = principal_amount * (1 + nominal_percentage_rate /
                         num_times_per_year) ** (num_times_per_year*years)
    return a

def final_amount_v3(amount, rate, compounded, years):
    a = amount * (1 + rate/compounded) ** (componded*years)
    return a

def final_amount_v4(amount, rate, compounded, years):
    """
    The a in final_amount_v3 was a useless asignment.
    We might as well skip it.
    """
    return amount * (1 + rate/compounded) ** (componded*years)

They all do the same thing. Use your judgement to write code that can be best understood by other humans! Short variable names should generally be avoided, unless when short variables make more sense. This happens in particular with mathematical equations, where it’s perfectly fine to use x, y, etc.

4.6. Variables and parameters are local

When we create a local variable inside a function, it only exists inside the function, and we cannot use it outside. For example, consider again this function:

def final_amount(p, r, n, t):
    a = p * (1 + r/n) ** (n*t)
    return a

If we try to use a, outside the function, we’ll get an error:

>>> a
NameError: name 'a' is not defined

The variable a is local to final_amount, and is not visible outside the function.

Additionally, a only exists while the function is being executed — we call this its lifetime. When the execution of the function terminates, the local variables are destroyed.

Parameters are also local, and act like local variables. For example, the lifetimes of p, r, n, t begin when final_amount is called, and the lifetime ends when the function completes its execution.

So it is not possible for a function to set some local variable to a value, complete its execution, and then when it is called again next time, recover the local variable. Each call of the function creates new local variables, and their lifetimes expire when the function returns to the caller.

4.7. Turtles Revisited

Now that we have fruitful functions, we can focus our attention on reorganizing our code so that it fits more nicely into our mental chunks. This process of rearrangement is called refactoring the code.

Two things we’re always going to want to do when working with turtles is to create the window for the turtle, and to create one or more turtles. We could write some functions to make these tasks easier in future:

import turtle

def make_window(color, title):
    """
      Set up the window with the given background color and title.
      Returns the new window.
    """
    window = turtle.Screen()
    window.bgcolor(color)
    window.title(title)
    return window


def make_turtle(color, size):
    """
      Set up a turtle with the given color and pensize.
      Returns the new turtle.
    """
    animal = turtle.Turtle()
    animal.color(color)
    animal.pensize(size)
    return animal


wn = make_window("lightgreen", "Tess and Alex dancing")
tess = make_turtle("hotpink", 5)
alex = make_turtle("black", 1)
dave = make_turtle("yellow", 2)

The trick about refactoring code is to anticipate which things we are likely to want to change each time we call the function: these should become the parameters, or changeable parts, of the functions we write.

4.8. Glossary

argument

A value provided to a function when the function is called. This value is assigned to the corresponding parameter in the function. The argument can be the result of an expression which may involve operators, operands and calls to other fruitful functions.

body

The second part of a compound statement. The body consists of a sequence of statements all indented the same amount from the beginning of the header. The standard amount of indentation used within the Python community is 4 spaces.

compound statement

A statement that consists of two parts:

1. header - which begins with a keyword determining the statement type, and ends with a colon.
2. body - containing one or more statements indented the same amount from the header.

The syntax of a compound statement looks like this:

keyword ... :
    statement
    statement ...

docstring

A special string that is attached to a function as its __doc__ attribute. Tools like Spyder can use docstrings to provide documentation or hints for the programmer. When we get to modules, classes, and methods, we’ll see that docstrings can also be used there.

flow of execution

The order in which statements are executed during a program run.

frame

A box in a stack diagram that represents a function call. It contains the local variables and parameters of the function.

function

A named sequence of statements that performs some useful operation. Functions may or may not take parameters and may or may not produce a result.

function call

A statement that executes a function. It consists of the name of the function followed by a list of arguments enclosed in parentheses.

function composition

Using the output from one function call as the input to another.

function definition

A statement that creates a new function, specifying its name, parameters, and the statements it executes.

fruitful function

A function that returns a value when it is called.

header line

The first part of a compound statement. A header line begins with a keyword and ends with a colon (:)

import statement

A statement which permits functions and variables defined in another Python module to be brought into the environment of another script. To use the features of the turtle, we need to first import the turtle module.

lifetime

Variables and objects have lifetimes — they are created at some point during program execution, and will be destroyed at some time.

local variable

A variable defined inside a function. A local variable can only be used inside its function. Parameters of a function are also a special kind of local variable.

parameter

A name used inside a function to refer to the value which was passed to it as an argument.

refactor

A fancy word to describe reorganizing our program code, usually to make it more understandable. Typically, we have a program that is already working, then we go back to “tidy it up”. It often involves choosing better variable names, or spotting repeated patterns and moving that code into a function.

stack diagram

A graphical representation of a stack of functions, their variables, and the values to which they refer.

traceback

A list of the functions that are executing, printed when a runtime error occurs. A traceback is also commonly refered to as a stack trace, since it lists the functions in the order in which they are stored in the runtime stack.

void function

The opposite of a fruitful function: one that does not return a value. It is executed for the work it does, rather than for the value it returns.

4.9. Exercises

1. Write a void (non-fruitful) function to draw a square. Use it in a program to draw the image shown below. Assume each side is 20 units. (Hint: notice that the turtle has already moved away from the ending point of the last square when the program ends.)

   

2. Write a program to draw this. Assume the innermost square is 20 units per side, and each successive square is 20 units bigger, per side, than the one inside it.

   

3. Write a void function draw_poly(t, n, sz) which makes a turtle draw a regular polygon. When called with draw_poly(tess, 8, 50), it will draw a shape like this:

   

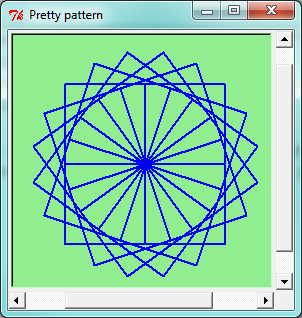
4. Draw this pretty pattern.

   

5. The two spirals in this picture differ only by the turn angle. Draw both.

   

6. Write a void function draw_equitriangle(t, sz) which calls draw_poly from the previous question to have its turtle draw a equilateral triangle.

7. Write a fruitful function sum_to(n) that returns the sum of all integer numbers up to and including n. So sum_to(10) would be 1+2+3…+10 which would return the value 55.

8. Write a function area_of_circle(r) which returns the area of a circle of radius r.

9. Write a void function to draw a star, where the length of each side is 100 units. (Hint: You should turn the turtle by 144 degrees at each point.)

   

10. Extend your program above. Draw five stars, but between each, pick up the pen, move forward by 350 units, turn right by 144, put the pen down, and draw the next star. You’ll get something like this:

    

    What would it look like if you didn’t pick up the pen?

4.9.1. Fruitful functions

4.10. Return values

The built-in functions we have used, such as abs, pow, int, max, and range, have produced results. Calling each of these functions generates a value, which we usually assign to a variable or use as part of an expression.

biggest = max(3, 7, 2, 5)
x = abs(3 - 11) + 10

We also wrote our own function to return the final amount for a compound interest calculation.

In this chapter, we are going to write more functions that return values, which we will call fruitful functions, for want of a better name. The first example is area, which returns the area of a circle with the given radius:

def area(radius):
    b = 3.14159 * radius**2
    return b

We have seen the return statement before, but in a fruitful function the return statement includes a return value. This statement means: evaluate the return expression, and then return it immediately as the result (the fruit) of this function. The expression provided can be arbitrarily complicated, so we could have written this function like this:

def area(radius):
    return 3.14159 * radius * radius

On the other hand, temporary variables like b above often make debugging easier.

Sometimes it is useful to have multiple return statements, one in each branch of a conditional. We have already seen the built-in abs, now we see how to write our own:

def absolute_value(x):
    if x < 0:
        return -x
    else:
        return x

Another way to write the above function is to leave out the else and just follow the if condition by the second return statement.

def absolute_value(x):
    if x < 0:
        return -x
    return x

Think about this version and convince yourself it works the same as the first one.

Code that appears after a return statement, or any other place the flow of execution can never reach, is called dead code, or unreachable code.

In a fruitful function, it is a good idea to ensure that every possible path through the program hits a return statement. The following version of absolute_value fails to do this:

def bad_absolute_value(x):
    if x < 0:
        return -x
    elif x > 0:
        return x

This version is not correct because if x happens to be 0, neither condition is true, and the function ends without hitting a return statement. In this case, the return value is a special value called None:

>>> print(bad_absolute_value(0))
None

All Python functions return None whenever they do not return another value.

It is also possible to use a return statement in the middle of a for loop, in which case control immediately returns from the function. Let us assume that we want a function which looks through a list of words. It should return the first 2-letter word. If there is not one, it should return the empty string:

def find_first_2_letter_word(words):
    for word in words:
        if len(word) == 2:
           return word
    return ""

>>> find_first_2_letter_word(["This",  "is", "a", "dead", "parrot"])
'is'
>>> find_first_2_letter_word(["I",  "like",  "cheese"])
''

Single-step through this code and convince yourself that in the first test case that we’ve provided, the function returns while processing the second element in the list: it does not have to traverse the whole list.

4.11. Program development

At this point, you should be able to look at complete functions and tell what they do. Also, if you have been doing the exercises, you have written some small functions. As you write larger functions, you might start to have more difficulty, especially with runtime and semantic errors.

To deal with increasingly complex programs, we are going to suggest a technique called incremental development. The goal of incremental development is to avoid long debugging sessions by adding and testing only a small amount of code at a time.

As an example, suppose we want to find the distance between two points, given by the coordinates (x₁, y₁) and (x₂, y₂). By the Pythagorean theorem, the distance is:

The first step is to consider what a distance function should look like in Python. In other words, what are the inputs (parameters) and what is the output (return value)?

In this case, the two points are the inputs, which we can represent using four parameters. The return value is the distance, which is a floating-point value.

Already we can write an outline of the function that captures our thinking so far:

def distance(x1, y1, x2, y2):
    return 0.0

Obviously, this version of the function doesn’t compute distances; it always returns zero. But it is syntactically correct, and it will run, which means that we can test it before we make it more complicated.

To test the new function, we call it with sample values:

>>> distance(1, 2, 4, 6)
0.0

We chose these values so that the horizontal distance equals 3 and the vertical distance equals 4; that way, the result is 5 (the hypotenuse of a 3-4-5 triangle). When testing a function, it is useful to know the right answer.

At this point we have confirmed that the function is syntactically correct, and we can start adding lines of code. After each incremental change, we test the function again. If an error occurs at any point, we know where it must be — in the last line we added.

A logical first step in the computation is to find the differences x₂- x₁ and y₂- y₁. We will refer to those values using temporary variables named dx and dy.

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    return 0.0

If we call the function with the arguments shown above, when the flow of execution gets to the return statement, dx should be 3 and dy should be 4. We can check this by running the function and printing the returned variable.

Next we compute the sum of squares of dx and dy:

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquared = dx*dx + dy*dy
    return 0.0

Again, we could run the program at this stage and check the value of dsquared (which should be 25).

Finally, using the fractional exponent 0.5 to find the square root, we compute and return the result:

def distance(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dsquared = dx*dx + dy*dy
    result = dsquared**0.5
    return result

If that works correctly, you are done. Otherwise, you might want to inspect the value of result before the return statement.

When you start out, you might add only a line or two of code at a time. As you gain more experience, you might find yourself writing and debugging bigger conceptual chunks. Either way, stepping through your code one line at a time and verifying that each step matches your expectations can save you a lot of debugging time. As you improve your programming skills you should find yourself managing bigger and bigger chunks: this is very similar to the way we learned to read letters, syllables, words, phrases, sentences, paragraphs, etc., or the way we learn to chunk music — from individual notes to chords, bars, phrases, and so on.

The key aspects of the process are:

1. Start with a working skeleton program and make small incremental changes. At any point, if there is an error, you will know exactly where it is.
2. Use temporary variables to refer to intermediate values so that you can easily inspect and check them.
3. Once the program is working, relax, sit back, and play around with your options. (There is interesting research that links “playfulness” to better understanding, better learning, more enjoyment, and a more positive mindset about what you can achieve — so spend some time fiddling around!) You might want to consolidate multiple statements into one bigger compound expression, or rename the variables you’ve used, or see if you can make the function shorter. A good guideline is to aim for making code as easy as possible for others to read.

Here is another version of the function. It makes use of a square root function that is in the math module (we’ll learn about modules shortly). Which do you prefer? Which looks “closer” to the Pythagorean formula we started out with?

import math

def distance(x1, y1, x2, y2):
    return math.sqrt( (x2-x1)**2 + (y2-y1)**2 )

>>> distance(1, 2, 4, 6)
5.0

4.12. Debugging with print

A powerful technique for debugging, is to insert extra print functions in carefully selected places in your code. Then, by inspecting the output of the program, you can check whether the algorithm is doing what you expect it to. Be clear about the following, however:

• You must have a clear solution to the problem, and must know what should happen before you can debug a program. Work on solving the problem on a piece of paper (perhaps using a flowchart to record the steps you take) before you concern yourself with writing code. Writing a program doesn’t solve the problem — it simply automates the manual steps you would take. So first make sure you have a pen-and-paper manual solution that works. Programming then is about making those manual steps happen automatically.

• Do not write chatterbox functions. A chatterbox is a fruitful function that, in addition to its primary task, also asks the user for input, or prints output, when it would be more useful if it simply shut up and did its work quietly.

  For example, we’ve seen built-in functions like range, max and abs. None of these would be useful building blocks for other programs if they prompted the user for input, or printed their results while they performed their tasks.

  So a good tip is to avoid calling print and input functions inside fruitful functions, unless the primary purpose of your function is to perform input and output. The one exception to this rule might be to temporarily sprinkle some calls to print into your code to help debug and understand what is happening when the code runs, but these will then be removed once you get things working.

4.13. Composition

As you should expect by now, you can call one function from within another. This ability is called composition.

As an example, we’ll write a function that takes two points, the center of the circle and a point on the perimeter, and computes the area of the circle.

Assume that the center point is stored in the variables xc and yc, and the perimeter point is in xp and yp. The first step is to find the radius of the circle, which is the distance between the two points. Fortunately, we’ve just written a function, distance, that does just that, so now all we have to do is use it:

radius = distance(xc, yc, xp, yp)

The second step is to find the area of a circle with that radius and return it. Again we will use one of our earlier functions:

result = area(radius)
return result

Wrapping that up in a function, we get:

def area_of_circle(xc, yc, xp, yp):
    radius = distance(xc, yc, xp, yp)
    result = area(radius)
    return result

The temporary variables radius and result are useful for development, debugging, and single-stepping through the code to inspect what is happening, but once the program is working, we can make it more concise by composing the function calls:

def area_of_circle(xc, yc, xp, yp):
    return area(distance(xc, yc, xp, yp))

4.14. Boolean functions

Functions can return Boolean values, which is often convenient for hiding complicated tests inside functions. For example:

def is_divisible(x, y):
    """ Test if x is exactly divisible by y """
    if x % y == 0:
        return True
    else:
        return False

It is common to give Boolean functions names that sound like yes/no questions. is_divisible returns either True or False to indicate whether the x is or is not divisible by y.

We can make the function more concise by taking advantage of the fact that the condition of the if statement is itself a Boolean expression. We can return it directly, avoiding the if statement altogether:

def is_divisible(x, y):
    return x % y == 0

This session shows the new function in action:

>>> is_divisible(6, 4)
False
>>> is_divisible(6, 3)
True

Boolean functions are often used in conditional statements:

if is_divisible(x, y):
    ... # Do something ...
else:
    ... # Do something else ...

It might be tempting to write something like:

if is_divisible(x, y) == True:

but the extra comparison is unnecessary.

4.15. Programming with style

Readability is very important to programmers, since in practice programs are read and modified far more often then they are written. But, like most rules, we occasionaly break them. Most of the code examples in this book will be consistent with the Python Enhancement Proposal 8 (PEP 8), a style guide developed by the Python community.

We’ll have more to say about style as our programs become more complex, but a few pointers will be helpful already:

• use 4 spaces (instead of tabs) for indentation
• limit line length to 78 characters
• when naming identifiers, use CamelCase for classes (we’ll get to those) and lowercase_with_underscores for functions and variables
• place imports at the top of the file
• keep function definitions together below the import statements
• use docstrings to document functions
• use two blank lines to separate function definitions from each other
• keep top level statements, including function calls, together at the bottom of the program

4.16. Glossary

Boolean function

A function that returns a Boolean value. The only possible values of the bool type are False and True.

chatterbox function

A function which interacts with the user (using input or print) when it should not. Silent functions that just convert their input arguments into their output results are usually the most useful ones.

composition (of functions)

Calling one function from within the body of another, or using the return value of one function as an argument to the call of another.

dead code

Part of a program that can never be executed, often because it appears after a return statement.

fruitful function

A function that yields a return value instead of None.

incremental development

A program development plan intended to simplify debugging by adding and testing only a small amount of code at a time.

None

A special Python value. One use in Python is that it is returned by functions that do not execute a return statement with a return argument.

return value

The value provided as the result of a function call.

scaffolding

Code that is used during program development to assist with development and debugging. The unit test code that we added in this chapter are examples of scaffolding.

temporary variable

A variable used to store an intermediate value in a complex calculation.

4.17. Exercises

After completing each exercise, confirm that all the tests pass.

1. The four compass points can be abbreviated by single-letter strings as “N”, “E”, “S”, and “W”. Write a function turn_clockwise that takes one of these four compass points as its parameter, and returns the next compass point in the clockwise direction. Here are some tests that should pass:

   >>>turn_clockwise("N") == "E"
   True
   >>>turn_clockwise("W") == "N"
   True
   

   You might ask “What if the argument to the function is some other value?” For all other cases, the function should return the value None.

2. Write a function day_name that converts an integer number 0 to 6 into the name of a day. Assume day 0 is “Sunday”. Once again, return None if the arguments to the function are not valid.

3. Write the inverse function day_num which is given a day name, and returns its number.

   Once again, if this function is given an invalid argument, it should return None.

4. Write a function that helps answer questions like ‘“Today is Wednesday. I leave on holiday in 19 days time. What day will that be?”’ So the function must take a day name and a delta argument — the number of days to add — and should return the resulting day name:

   day_add("Monday", 4) ==  "Friday"
   day_add("Tuesday", 0) == "Tuesday"
   day_add("Tuesday", 14) == "Tuesday"
   day_add("Sunday", 100) == "Tuesday"
   

   Hint: use the first two functions written above to help you write this one.

5. Can your day_add function already work with negative deltas? For example, -1 would be yesterday, or -7 would be a week ago:

   day_add("Sunday", -1) == "Saturday"
   day_add("Sunday", -7) == "Sunday"
   day_add("Tuesday", -100) == "Sunday"
   

   If your function already works, explain why. If it does not work, make it work.

   Hint: Play with some cases of using the modulus function % (introduced at the beginning of the previous chapter). Specifically, explore what happens to x % 7 when x is negative.

6. Write a function days_in_month which takes the name of a month, and returns the number of days in the month. Ignore leap years:

   days_in_month("February") == 28
   days_in_month("December") == 31
   

   If the function is given invalid arguments, it should return None.

7. Write a function to_secs that converts hours, minutes and seconds to a total number of seconds. Here are some tests that should pass:

   to_secs(2, 30, 10) == 9010
   to_secs(2, 0, 0) == 7200
   to_secs(0, 2, 0) == 120
   to_secs(0, 0, 42) == 42
   to_secs(0, -10, 10) == -590
   

8. Extend to_secs so that it can cope with real values as inputs. It should always return an integer number of seconds (truncated towards zero):

   to_secs(2.5, 0, 10.71) == 9010
   to_secs(2.433,0,0) == 8758
   

9. Write three functions that are the “inverses” of to_secs:

   1. hours_in returns the whole integer number of hours represented by a total number of seconds.
   2. minutes_in returns the whole integer number of left over minutes in a total number of seconds, once the hours have been taken out.
   3. seconds_in returns the left over seconds represented by a total number of seconds.

   You may assume that the total number of seconds passed to these functions is an integer. Here are some test cases:

   hours_in(9010) == 2
   minutes_in(9010) == 30
   seconds_in(9010) == 10
   

10. Which of these tests fail? Explain why.

    3 % 4 == 0
    3 % 4 == 3
    3 / 4 == 0
    3 // 4 == 0
    3+4  *  2 == 14
    4-2+2 == 0
    len("hello, world!") == 13
    

11. Write a compare function that returns 1 if a > b, 0 if a == b, and -1 if a < b

    compare(5, 4) == 1
    compare(7, 7) == 0
    compare(2, 3) == -1
    compare(42, 1) == 1
    

12. Write a function called hypotenuse that returns the length of the hypotenuse of a right triangle given the lengths of the two legs as parameters:

    hypotenuse(3, 4) == 5.0
    hypotenuse(12, 5) == 13.0
    hypotenuse(24, 7) == 25.0
    hypotenuse(9, 12) == 15.0
    

13. Write a function slope(x1, y1, x2, y2) that returns the slope of the line through the points (x1, y1) and (x2, y2). Be sure your implementation of slope can pass the following tests:

    slope(5, 3, 4, 2) == 1.0
    slope(1, 2, 3, 2) == 0.0
    slope(1, 2, 3, 3) == 0.5
    slope(2, 4, 1, 2) == 2.0
    

    Then use a call to slope in a new function named intercept(x1, y1, x2, y2) that returns the y-intercept of the line through the points (x1, y1) and (x2, y2)

    intercept(1, 6, 3, 12) == 3.0
    intercept(6, 1, 1, 6) == 7.0
    intercept(4, 6, 12, 8) == 5.0
    

14. Write a function called is_even(n) that takes an integer as an argument and returns True if the argument is an even number and False if it is odd.

    Add your own tests to the test suite.

15. Now write the function is_odd(n) that returns True when n is odd and False otherwise. Include unit tests for this function too.

    Finally, modify it so that it uses a call to is_even to determine if its argument is an odd integer, and ensure that its test still pass.

16. Write a function is_factor(f, n) that passes these tests:

    is_factor(3, 12)
    not is_factor(5, 12)
    is_factor(7, 14)
    not is_factor(7, 15)
    is_factor(1, 15)
    is_factor(15, 15)
    not is_factor(25, 15)
    

17. Write is_multiple to satisfy these statements using is_factor from the previous execise.

    is_multiple(12, 3) is_multiple(12, 4) not is_multiple(12, 5) is_multiple(12, 6) not is_multiple(12, 7)

18. Write the function f2c(t) designed to return the integer value of the nearest degree Celsius for given temperature in Fahrenheit. (hint: you may want to make use of the built-in function, round. Try printing round.__doc__ in a Python shell or looking up help for the round function, and experimenting with it until you are comfortable with how it works.)

    f2c(212) == 100     # Boiling point of water
    f2c(32) == 0        # Freezing point of water
    f2c(-40) == -40     # Wow, what an interesting case!
    f2c(36) == 2
    f2c(37) == 3
    f2c(38) == 3
    f2c(39) == 4
    

19. Now do the opposite: write the function c2f which converts Celsius to Fahrenheit:

    c2f(0) == 32
    c2f(100) == 212
    c2f(-40) == -40
    c2f(12) == 54
    c2f(18) == 64
    c2f(-48) == -54
    

4.17.1. Modifiers vs Pure Functions

Functions which take lists as arguments and change them during execution are called modifiers and the changes they make are called side effects.

A pure function does not produce side effects. It communicates with the calling program only through parameters, which it does not modify, and a return value. Let’s make a function which doubles the items in a list:

def double_stuff(values):
    """ Return a new list which contains
        doubles of the elements in the list values.
    """
    new_list = []
    for value in values:
        new_elem = 2 * value
        new_list.append(new_elem)

    return new_list

This version of double_stuff does not change its arguments:

>>> things = [2, 5, 9]
>>> more_things = double_stuff(things)
>>> things
[2, 5, 9]
>>> more_things
[4, 10, 18]

An early rule we saw for assignment said “first evaluate the right hand side, then assign the resulting value to the variable”. So it is quite safe to assign the function result to the same variable that was passed to the function:

>>> things = [2, 5, 9]
>>> things = double_stuff(things)
>>> things
[4, 10, 18]

If however, we change the definition of double_stuff to the following:

def double_stuff(values):
    """ Double the elements of values in-place. """
    for index, value in enumerate(values):
        values[index] = 2 * value

We get upon execution:

>>> things = [2, 5, 9]
>>> more_things = double_stuff(things)
>>> things
[4, 10, 18]
>>> more_things
None

We see that the original list was modified, while the function doesn’t return anything. This is a good idea when building modifiers.

Which style is better?

In general, we recommend that you always use pure functions, and only use modifiers when you are prepared to stick your head into a lion’s mouth, and have thought about the risks.

4.17.2. Some Tips, Tricks, and Common Errors

These are small summaries of ideas, tips, and commonly seen errors that might be helpful to those beginning Python.

4.18. Functions

Functions help us with our mental chunking: they allow us to group together statements for a high-level purpose, e.g. a function to sort a list of items, a function to make the turtle draw a spiral, or a function to compute the mean and standard deviation of some measurements.

There are two kinds of functions: fruitful, or value-returning functions, which calculate and return a value, and we use them because we’re primarily interested in the value they’ll return. Void (non-fruitful) functions are used because they perform actions that we want done — e.g. make a turtle draw a rectangle, or print the first thousand prime numbers. They always return None — a special dummy value.

Tip: None is not a string

Values like None, True and False are not strings: they are special values in Python, and are in the list of keywords we gave in chapter 2 (Variables, expressions, and statements). Keywords are special in the language: they are part of the syntax. So we cannot create our own variable or function with a name True — we’ll get a syntax error. (Built-in functions are not privileged like keywords: we can define our own variable or function called len, but we’d be silly to do so!)

Along with the fruitful/void families of functions, there are two flavors of the return statement in Python: one that returns a useful value, and the other that returns nothing, or None. And if we get to the end of any function and we have not explicitly executed any return statement, Python automatically returns the value None.

Tip: Understand what the function needs to return

Perhaps nothing — some functions exists purely to perform actions rather than to calculate and return a result. But if the function should return a value, make sure all execution paths do return the value.

To make functions more useful, they are given parameters. So a function to make a turtle draw a square might have two parameters — one for the turtle that needs to do the drawing, and another for the size of the square. See the first example in Chapter 4 (Functions) — that function can be used with any turtle, and for any size square. So it is much more general than a function that always uses a specific turtle, say tess to draw a square of a specific size, say 30.

Tip: Use parameters to generalize functions

Understand which parts of the function will be hard-coded and unchangeable, and which parts should become parameters so that they can be customized by the caller of the function.

Tip: Try to relate Python functions to ideas we already know

In math, we’re familiar with functions like f(x) = 3x + 5. We already understand that when we call the function f(3) we make some association between the parameter x and the argument 3. Try to draw parallels to argument passing in Python.

Quiz: Is the function f(z) = 3z + 5 the same as function f above?

4.19. Problems with logic and flow of control

We often want to know if some condition holds for any item in a list, e.g. “does the list have any odd numbers?” This is a common mistake:

def any_odd(xs):  # Buggy version
    """ Return True if there is an odd number in xs, a list of integers. """
    for v in xs:
       if v % 2 == 1:
           return True
       else:
           return False

Can we spot two problems here? As soon as we execute a return, we’ll leave the function. So the logic of saying “If I find an odd number I can return True” is fine. However, we cannot return False after only looking at one item — we can only return False if we’ve been through all the items, and none of them are odd. So line 6 should not be there, and line 7 has to be outside the loop. To find the second problem above, consider what happens if you call this function with an argument that is an empty list. Here is a corrected version:

def any_odd(xs):
    """ Return True if there is an odd number in xs, a list of integers. """
    for v in xs:
       if v % 2 == 1:
           return True
    return False

This “eureka”, or “short-circuit” style of returning from a function as soon as we are certain what the outcome will be was first seen in Section 8.10, in the chapter on strings.

It is preferred over this one, which also works correctly:

def any_odd(xs):
    """ Return True if there is an odd number in xs, a list of integers. """
    count = 0
    for v in xs:
       if v % 2 == 1:
          count += 1    # Count the odd numbers
    if count > 0:
       return True
    else:
       return False

The performance disadvantage of this one is that it traverses the whole list, even if it knows the outcome very early on.

Tip: Think about the return conditions of the function

Do I need to look at all elements in all cases? Can I shortcut and take an early exit? Under what conditions? When will I have to examine all the items in the list?

The code in lines 7-10 can also be tightened up. The expression count > 0 evaluates to a Boolean value, either True or False. The value can be used directly in the return statement. So we could cut out that code and simply have the following:

def any_odd(xs):
    """ Return True if there is an odd number in xs, a list of integers. """
    count = 0
    for v in xs:
       if v % 2 == 1:
          count += 1   # Count the odd numbers
    return count > 0   # Aha! a programmer who understands that Boolean
                       #   expressions are not just used in if statements!

Although this code is tighter, it is not as nice as the one that did the short-circuit return as soon as the first odd number was found.

Tip: Generalize your use of Booleans

Mature programmers won’t write if is_prime(n) == True: when they could say instead if is_prime(n): Think more generally about Boolean values, not just in the context of if or while statements. Like arithmetic expressions, they have their own set of operators (and, or, not) and values (True, False) and can be assigned to variables, put into lists, etc. A good resource for improving your use of Booleans is http://en.wikibooks.org/wiki/Non-Programmer%27s_Tutorial_for_Python_3/Boolean_Expressions

Exercise time:

• How would we adapt this to make another function which returns True if all the numbers are odd? Can you still use a short-circuit style?
• How would we adapt it to return True if at least three of the numbers are odd? Short-circuit the traversal when the third odd number is found — don’t traverse the whole list unless we have to.

4.20. Local variables

Functions are called, or activated, and while they’re busy they create their own stack frame which holds local variables. A local variable is one that belongs to the current activation. As soon as the function returns (whether from an explicit return statement or because Python reached the last statement), the stack frame and its local variables are all destroyed. The important consequence of this is that a function cannot use its own variables to remember any kind of state between different activations. It cannot count how many times it has been called, or remember to switch colors between red and blue UNLESS it makes use of variables that are global. Global variables will survive even after our function has exited, so they are the correct way to maintain information between calls.

sz = 2
def h2():
    """ Draw the next step of a spiral on each call. """
    global sz
    tess.turn(42)
    tess.forward(sz)
    sz += 1

This fragment assumes our turtle is tess. Each time we call h2() it turns, draws, and increases the global variable sz. Python always assumes that an assignment to a variable (as in line 7) means that we want a new local variable, unless we’ve provided a global declaration (on line 4). So leaving out the global declaration means this does not work.

Tip: Local variables do not survive when you exit the function

Use a Python visualizer like the one at http://netserv.ict.ru.ac.za/python3_viz to build a strong understanding of function calls, stack frames, local variables, and function returns.

Tip: Assignment in a function creates a local variable

Any assignment to a variable within a function means Python will make a local variable, unless we override with global.

4.21. String handling

There are only four really important operations on strings, and we’ll be able to do just about anything. There are many more nice-to-have methods (we’ll call them sugar coating) that can make life easier, but if we can work with the basic four operations smoothly, we’ll have a great grounding.

• len(str) finds the length of a string.
• str[i] the subscript operation extracts the i’th character of the string, as a new string.
• str[i:j] the slice operation extracts a substring out of a string.
• str.find(target) returns the index where target occurs within the string, or -1 if it is not found.

So if we need to know if “snake” occurs as a substring within s, we could write

if s.find("snake") >= 0:  ...
if "snake" in s: ...           # Also works, nice-to-know sugar coating!

It would be wrong to split the string into words unless we were asked whether the word “snake” occurred in the string.

Suppose we’re asked to read some lines of data and find function definitions, e.g.: def some_function_name(x, y):, and we are further asked to isolate and work with the name of the function. (Let’s say, print it.)

s = "..."                         # Get the next line from somewhere
def_pos = s.find("def ")          # Look for "def " in the line
if def_pos == 0:                  # If it occurs at the left margin
  op_index = s.find("(")          # Find the index of the open parenthesis
  fnname = s[4:op_index]          # Slice out the function name
  print(fnname)                   # ... and work with it.

One can extend these ideas:

• What if the function def was indented, and didn’t start at column 0? The code would need a bit of adjustment, and we’d probably want to be sure that all the characters in front of the def_pos position were spaces. We would not want to do the wrong thing on data like this: # I def initely like Python!
• We’ve assumed on line 3 that we will find an open parenthesis. It may need to be checked that we did!
• We have also assumed that there was exactly one space between the keyword def and the start of the function name. It will not work nicely for def       f(x)

As we’ve already mentioned, there are many more “sugar-coated” methods that let us work more easily with strings. There is an rfind method, like find, that searches from the end of the string backwards. It is useful if we want to find the last occurrence of something. The lower and upper methods can do case conversion. And the split method is great for breaking a string into a list of words, or into a list of lines. We’ve also made extensive use in this book of the format method. In fact, if we want to practice reading the Python documentation and learning some new methods on our own, the string methods are an excellent resource.

Exercises:

• Suppose any line of text can contain at most one url that starts with “http://” and ends at the next space in the line. Write a fragment of code to extract and print the full url if it is present. (Hint: read the documentation for find. It takes some extra arguments, so you can set a starting point from which it will search.)
• Suppose a string contains at most one substring “< … >”. Write a fragment of code to extract and print the portion of the string between the angle brackets.

4.22. Looping and lists

Computers are useful because they can repeat computation, accurately and fast. So loops are going to be a central feature of almost all programs you encounter.

Tip: Don’t create unnecessary lists

Lists are useful if you need to keep data for later computation. But if you don’t need lists, it is probably better not to generate them.

Here are two functions that both generate ten million random numbers, and return the sum of the numbers. They both work.

import random
joe = random.Random()

def sum1():
   """ Build a list of random numbers, then sum them """
   xs = []
   for i in range(10000000):
       num = joe.randrange(1000)  # Generate one random number
       xs.append(num)             # Save it in our list

   tot = sum(xs)
   return tot

def sum2():
   """ Sum the random numbers as we generate them """
   tot = 0
   for i in range(10000000):
       num = joe.randrange(1000)
       tot += num
   return tot

print(sum1())
print(sum2())

What reasons are there for preferring the second version here? (Hint: open a tool like the Performance Monitor on your computer, and watch the memory usage. How big can you make the list before you get a fatal memory error in sum1?)

In a similar way, when working with files, we often have an option to read the whole file contents into a single string, or we can read one line at a time and process each line as we read it. Line-at-a-time is the more traditional and perhaps safer way to do things — you’ll be able to work comfortably no matter how large the file is. (And, of course, this mode of processing the files was essential in the old days when computer memories were much smaller.) But you may find whole-file-at-once is sometimes more convenient!