Classes and Objects

Classes and Objects — the Basics

Object-oriented programming

Python is an object-oriented programming language, which means that it provides features that support object-oriented programming (OOP).

Object-oriented programming has its roots in the 1960s, but it wasn’t until the mid 1980s that it became the main programming paradigm used in the creation of new software. It was developed as a way to handle the rapidly increasing size and complexity of software systems, and to make it easier to modify these large and complex systems over time.

Up to now, most of the programs we have been writing use a procedural programming paradigm. In procedural programming the focus is on writing functions or procedures which operate on data. In object-oriented programming the focus is on the creation of objects which contain both data and functionality together. (We have seen turtle objects, string objects, and random number generators, to name a few places where we’ve already worked with objects.)

Usually, each object definition corresponds to some object or concept in the real world, and the functions that operate on that object correspond to the ways real-world objects interact.

User-defined compound data types

We’ve already seen classes like str, int, float and Turtle. We are now ready to create our own user-defined class: the Point.

Consider the concept of a mathematical point. In two dimensions, a point is two numbers (coordinates) that are treated collectively as a single object. Points are often written in between parentheses with a comma separating the coordinates. For example, (0, 0) represents the origin, and (x, y) represents the point x units to the right and y units up from the origin.

Some of the typical operations that one associates with points might be calculating the distance of a point from the origin, or from another point, or finding a midpoint of two points, or asking if a point falls within a given rectangle or circle. We’ll shortly see how we can organize these together with the data.

A natural way to represent a point in Python is with two numeric values. The question, then, is how to group these two values into a compound object. The quick and dirty solution is to use a tuple, and for some applications that might be a good choice.

An alternative is to define a new class. This approach involves a bit more effort, but it has advantages that will be apparent soon. We’ll want our points to each have an x and a y attribute, so our first class definition looks like this:

class Point:
    """ Point class represents and manipulates x,y coords. """

    def __init__(self):
        """ Create a new point at the origin """
        self.x = 0
        self.y = 0

Class definitions can appear anywhere in a program, but they are usually near the beginning (after the import statements). Some programmers and languages prefer to put every class in a module of its own — we won’t do that here. The syntax rules for a class definition are the same as for other compound statements. There is a header which begins with the keyword, class, followed by the name of the class, and ending with a colon. Indentation levels tell us where the class ends.

If the first line after the class header is a string, it becomes the docstring of the class, and will be recognized by various tools. (This is also the way docstrings work in functions.)

Every class should have a method with the special name __init__. This initializer method is automatically called whenever a new instance of Point is created. It gives the programmer the opportunity to set up the attributes required within the new instance by giving them their initial state/values. The self parameter (we could choose any other name, but self is the convention) is automatically set to reference the newly created object that needs to be initialized.

So let’s use our new Point class now:

p = Point()         # Instantiate an object of type Point
q = Point()         # Make a second point

print(p.x, p.y, q.x, q.y)  # Each point object has its own x and y

This program prints:

0 0 0 0

because during the initialization of the objects, we created two attributes called x and y for each, and gave them both the value 0.

This should look familiar — we’ve used classes before to create more than one object:

from turtle import Turtle

tess = Turtle()     # Instantiate objects of type Turtle
alex = Turtle()

The variables p and q are assigned references to two new Point objects. A function like Turtle or Point that creates a new object instance is called a constructor, and every class automatically provides a constructor function which is named the same as the class.

It may be helpful to think of a class as a factory for making objects. The class itself isn’t an instance of a point, but it contains the machinery to make point instances. Every time we call the constructor, we’re asking the factory to make us a new object. As the object comes off the production line, its initialization method is executed to get the object properly set up with its factory default settings.

The combined process of “make me a new object” and “get its settings initialized to the factory default settings” is called instantiation.

Attributes

Like real world objects, object instances have both attributes and methods.

We can modify the attributes in an instance using dot notation:

>>> p.x = 3
>>> p.y = 4

Both modules and instances create their own namespaces, and the syntax for accessing names contained in each, called attributes, is the same. In this case the attribute we are selecting is a data item from an instance.

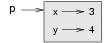
The following state diagram shows the result of these assignments:

The variable p refers to a Point object, which contains two attributes. Each attribute refers to a number.

We can access the value of an attribute using the same syntax:

>>> print(p.y)
4
>>> x = p.x
>>> print(x)
3

The expression p.x means, “Go to the object p refers to and get the value of x”. In this case, we assign that value to a variable named x. There is no conflict between the variable x (in the global namespace here) and the attribute x (in the namespace belonging to the instance). The purpose of dot notation is to fully qualify which variable we are referring to unambiguously.

We can use dot notation as part of any expression, so the following statements are legal:

print("(x={0}, y={1})".format(p.x, p.y))
distance_squared_from_origin = p.x * p.x + p.y * p.y

The first line outputs (x=3, y=4). The second line calculates the value 25.

Improving our initializer

To create a point at position (7, 6) currently needs three lines of code:

p = Point()
p.x = 7
p.y = 6

We can make our class constructor more general by placing extra parameters into the __init__ method, as shown in this example:

class Point:
    """ Point class represents and manipulates x,y coords. """

    def __init__(self, x=0, y=0):
        """ Create a new point at x, y """
        self.x = x
        self.y = y

# Other statements outside the class continue below here.

The x and y parameters here are both optional. If the caller does not supply arguments, they’ll get the default values of 0. Here is our improved class in action:

>>> p = Point(4, 2)
>>> q = Point(6, 3)
>>> r = Point()       # r represents the origin (0, 0)
>>> print(p.x, q.y, r.x)
4 3 0

Technically speaking …

If we are really fussy, we would argue that the __init__ method’s docstring is inaccurate. __init__ doesn’t create the object (i.e. set aside memory for it), — it just initializes the object to its factory-default settings after its creation.

But tools like PyScripter understand that instantiation — creation and initialization — happen together, and they choose to display the initializer’s docstring as the tooltip to guide the programmer that calls the class constructor.

So we’re writing the docstring so that it makes the most sense when it pops up to help the programmer who is using our Point class:

Adding other methods to our class

The key advantage of using a class like Point rather than a simple tuple (6, 7) now becomes apparent. We can add methods to the Point class that are sensible operations for points, but which may not be appropriate for other tuples like (25, 12) which might represent, say, a day and a month, e.g. Christmas day. So being able to calculate the distance from the origin is sensible for points, but not for (day, month) data. For (day, month) data, we’d like different operations, perhaps to find what day of the week it will fall on in 2020.

Creating a class like Point brings an exceptional amount of “organizational power” to our programs, and to our thinking. We can group together the sensible operations, and the kinds of data they apply to, and each instance of the class can have its own state.

A method behaves like a function but it is invoked on a specific instance, e.g. tess.right(90). Like a data attribute, methods are accessed using dot notation.

Let’s add another method, distance_from_origin, to see better how methods work:

class Point:
    """ Create a new Point, at coordinates x, y """

    def __init__(self, x=0, y=0):
        """ Create a new point at x, y """
        self.x = x
        self.y = y

    def distance_from_origin(self):
        """ Compute my distance from the origin """
        return ((self.x ** 2) + (self.y ** 2)) ** 0.5

Let’s create a few point instances, look at their attributes, and call our new method on them: (We must run our program first, to make our Point class available to the interpreter.)

>>> p = Point(3, 4)
>>> p.x
3
>>> p.y
4
>>> p.distance_from_origin()
5.0
>>> q = Point(5, 12)
>>> q.x
5
>>> q.y
12
>>> q.distance_from_origin()
13.0
>>> r = Point()
>>> r.x
0
>>> r.y
0
>>> r.distance_from_origin()
0.0

When defining a method, the first parameter refers to the instance being manipulated. As already noted, it is customary to name this parameter self.

Notice that the caller of distance_from_origin does not explicitly supply an argument to match the self parameter — this is done for us, behind our back.

Instances as arguments and parameters

We can pass an object as an argument in the usual way. We’ve already seen this in some of the turtle examples, where we passed the turtle to some function like draw_bar in the chapter titled Conditionals, so that the function could control and use whatever turtle instance we passed to it.

Be aware that our variable only holds a reference to an object, so passing tess into a function creates an alias: both the caller and the called function now have a reference, but there is only one turtle!

Here is a simple function involving our new Point objects:

def print_point(pt):
    print("({0}, {1})".format(pt.x, pt.y))

print_point takes a point as an argument and formats the output in whichever way we choose. If we call print_point(p) with point p as defined previously, the output is (3, 4).

Converting an instance to a string

Most object-oriented programmers probably would not do what we’ve just done in print_point. When we’re working with classes and objects, a preferred alternative is to add a new method to the class. And we don’t like chatterbox methods that call print. A better approach is to have a method so that every instance can produce a string representation of itself. Let’s initially call it to_string:

class Point:
    # ...

    def to_string(self):
        return "({0}, {1})".format(self.x, self.y)

Now we can say:

>>> p = Point(3, 4)
>>> print(p.to_string())
(3, 4)

But don’t we already have a str type converter that can turn our object into a string? Yes! And doesn’t print automatically use this when printing things? Yes again! But these automatic mechanisms do not yet do exactly what we want:

>>> str(p)
'<__main__.Point object at 0x01F9AA10>'
>>> print(p)
'<__main__.Point object at 0x01F9AA10>'

Python has a clever trick up its sleeve to fix this. If we call our new method __str__ instead of to_string, the Python interpreter will use our code whenever it needs to convert a Point to a string. Let’s re-do this again, now:

    class Point:
        # ...

        def __str__(self):    # All we have done is renamed the method
            return "({0}, {1})".format(self.x, self.y)

and now things are looking great!

>>> str(p)     # Python now uses the __str__ method that we wrote.
(3, 4)
>>> print(p)
(3, 4)

Instances as return values

Functions and methods can return instances. For example, given two Point objects, find their midpoint. First we’ll write this as a regular function:

def midpoint(p1, p2):
    """ Return the midpoint of points p1 and p2 """
    mx = (p1.x + p2.x)/2
    my = (p1.y + p2.y)/2
    return Point(mx, my)

The function creates and returns a new Point object:

>>> p = Point(3, 4)
>>> q = Point(5, 12)
>>> r = midpoint(p, q)
>>> r
(4.0, 8.0)

Now let us do this as a method instead. Suppose we have a point object, and wish to find the midpoint halfway between it and some other target point:

class Point:
   # ...

   def halfway(self, target):
        """ Return the halfway point between myself and the target """
        mx = (self.x + target.x)/2
        my = (self.y + target.y)/2
        return Point(mx, my)

This method is identical to the function, aside from some renaming. It’s usage might be like this:

>>> p = Point(3, 4)
>>> q = Point(5, 12)
>>> r = p.halfway(q)
>>> r
(4.0, 8.0)

While this example assigns each point to a variable, this need not be done. Just as function calls are composable, method calls and object instantiation are also composable, leading to this alternative that uses no variables:

>>> print(Point(3, 4).halfway(Point(5, 12)))
(4.0, 8.0)

A change of perspective

The original syntax for a function call, print_time(current_time), suggests that the function is the active agent. It says something like, “Hey, print_time! Here’s an object for you to print.”

In object-oriented programming, the objects are considered the active agents. An invocation like current_time.print_time() says “Hey current_time! Please print yourself!”

In our early introduction to turtles, we used an object-oriented style, so that we said tess.forward(100), which asks the turtle to move itself forward by the given number of steps.

This change in perspective might be more polite, but it may not initially be obvious that it is useful. But sometimes shifting responsibility from the functions onto the objects makes it possible to write more versatile functions, and makes it easier to maintain and reuse code.

The most important advantage of the object-oriented style is that it fits our mental chunking and real-life experience more accurately. In real life our cook method is part of our microwave oven — we don’t have a cook function sitting in the corner of the kitchen, into which we pass the microwave! Similarly, we use the cellphone’s own methods to send an sms, or to change its state to silent. The functionality of real-world objects tends to be tightly bound up inside the objects themselves. OOP allows us to accurately mirror this when we organize our programs.

Objects can have state

Objects are most useful when we also need to keep some state that is updated from time to time. Consider a turtle object. Its state consists of things like its position, its heading, its color, and its shape. A method like left(90) updates the turtle’s heading, forward changes its position, and so on.

For a bank account object, a main component of the state would be the current balance, and perhaps a log of all transactions. The methods would allow us to query the current balance, deposit new funds, or make a payment. Making a payment would include an amount, and a description, so that this could be added to the transaction log. We’d also want a method to show the transaction log.

Glossary

attribute

One of the named data items that makes up an instance.

class

A user-defined compound type. A class can also be thought of as a template for the objects that are instances of it. (The iPhone is a class. By December 2010, estimates are that 50 million instances had been sold!)

constructor

Every class has a “factory”, called by the same name as the class, for making new instances. If the class has an initializer method, this method is used to get the attributes (i.e. the state) of the new object properly set up.

initializer method

A special method in Python (called __init__) that is invoked automatically to set a newly created object’s attributes to their initial (factory-default) state.

instance

An object whose type is of some class. Instance and object are used interchangeably.

instantiate

To create an instance of a class, and to run its initializer.

method

A function that is defined inside a class definition and is invoked on instances of that class.

object

A compound data type that is often used to model a thing or concept in the real world. It bundles together the data and the operations that are relevant for that kind of data. Instance and object are used interchangeably.

object-oriented programming

A powerful style of programming in which data and the operations that manipulate it are organized into objects.

object-oriented language

A language that provides features, such as user-defined classes and inheritance, that facilitate object-oriented programming.

Exercises

1. Rewrite the distance function from the chapter titled Fruitful functions so that it takes two Points as parameters instead of four numbers.

2. Add a method reflect_x to Point which returns a new Point, one which is the reflection of the point about the x-axis. For example, Point(3, 5).reflect_x() is (3, -5)

3. Add a method slope_from_origin which returns the slope of the line joining the origin to the point. For example,

   >>> Point(4, 10).slope_from_origin()
   2.5
   

   What cases will cause this method to fail?

4. The equation of a straight line is “y = ax + b”, (or perhaps “y = mx + c”). The coefficients a and b completely describe the line. Write a method in the Point class so that if a point instance is given another point, it will compute the equation of the straight line joining the two points. It must return the two coefficients as a tuple of two values. For example,

   >>> print(Point(4, 11).get_line_to(Point(6, 15)))
   >>> (2, 3)
   

   This tells us that the equation of the line joining the two points is “y = 2x + 3”. When will this method fail?

5. Given four points that fall on the circumference of a circle, find the midpoint of the circle. When will this function fail?

   Hint: You must know how to solve the geometry problem before you think of going anywhere near programming. You cannot program a solution to a problem if you don’t understand what you want the computer to do!

6. Create a new class, SMS_store. The class will instantiate SMS_store objects, similar to an inbox or outbox on a cellphone:

   my_inbox = SMS_store()
   

   This store can hold multiple SMS messages (i.e. its internal state will just be a list of messages). Each message will be represented as a tuple:

   (has_been_viewed, from_number, time_arrived, text_of_SMS)
   

   The inbox object should provide these methods:

   my_inbox.add_new_arrival(from_number, time_arrived, text_of_SMS)
     # Makes new SMS tuple, inserts it after other messages
     # in the store. When creating this message, its
     # has_been_viewed status is set False.
   
   my_inbox.message_count()
     # Returns the number of sms messages in my_inbox
   
   my_inbox.get_unread_indexes()
     # Returns list of indexes of all not-yet-viewed SMS messages
   
   my_inbox.get_message(i)
     # Return (from_number, time_arrived, text_of_sms) for message[i]
     # Also change its state to "has been viewed".
     # If there is no message at position i, return None
   
   my_inbox.delete(i)     # Delete the message at index i
   my_inbox.clear()       # Delete all messages from inbox
   

   Write the class, create a message store object, write tests for these methods, and implement the methods.

Classes and Objects — Digging a little deeper

Rectangles

Let’s say that we want a class to represent a rectangle which is located somewhere in the XY plane. The question is, what information do we have to provide in order to specify such a rectangle? To keep things simple, assume that the rectangle is oriented either vertically or horizontally, never at an angle.

There are a few possibilities: we could specify the center of the rectangle (two coordinates) and its size (width and height); or we could specify one of the corners and the size; or we could specify two opposing corners. A conventional choice is to specify the upper-left corner of the rectangle, and the size.

Again, we’ll define a new class, and provide it with an initializer and a string converter method:

class Rectangle:
    """ A class to manufacture rectangle objects """

    def __init__(self, posn, w, h):
        """ Initialize rectangle at posn, with width w, height h """
        self.corner = posn
        self.width = w
        self.height = h

    def __str__(self):
        return  "({0}, {1}, {2})"
                  .format(self.corner, self.width, self.height)

box = Rectangle(Point(0, 0), 100, 200)
bomb = Rectangle(Point(100, 80), 5, 10)    # In my video game
print("box: ", box)
print("bomb: ", bomb)

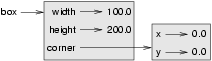
To specify the upper-left corner, we have embedded a Point object (as we used it in the previous chapter) within our new Rectangle object! We create two new Rectangle objects, and then print them producing:

box: ((0, 0), 100, 200)
bomb: ((100, 80), 5, 10)

The dot operator composes. The expression box.corner.x means, “Go to the object that box refers to and select its attribute named corner, then go to that object and select its attribute named x”.

The figure shows the state of this object:

Objects are mutable

We can change the state of an object by making an assignment to one of its attributes. For example, to grow the size of a rectangle without changing its position, we could modify the values of width and height:

box.width += 50
box.height += 100

Of course, we’d probably like to provide a method to encapsulate this inside the class. We will also provide another method to move the position of the rectangle elsewhere:

class Rectangle:
    # ...

    def grow(self, delta_width, delta_height):
        """ Grow (or shrink) this object by the deltas """
        self.width += delta_width
        self.height += delta_height

    def move(self, dx, dy):
        """ Move this object by the deltas """
        self.corner.x += dx
        self.corner.y += dy

Let us try this:

>>> r = Rectangle(Point(10,5), 100, 50)
>>> print(r)
((10, 5), 100, 50)
>>> r.grow(25, -10)
>>> print(r)
((10, 5), 125, 40)
>>> r.move(-10, 10)
print(r)
((0, 15), 125, 40)

Sameness

The meaning of the word “same” seems perfectly clear until we give it some thought, and then we realize there is more to it than we initially expected.

For example, if we say, “Alice and Bob have the same car”, we mean that her car and his are the same make and model, but that they are two different cars. If we say, “Alice and Bob have the same mother”, we mean that her mother and his are the same person.

When we talk about objects, there is a similar ambiguity. For example, if two Points are the same, does that mean they contain the same data (coordinates) or that they are actually the same object?

We’ve already seen the is operator in the chapter on lists, where we talked about aliases: it allows us to find out if two references refer to the same object:

>>> p1 = Point(3, 4)
>>> p2 = Point(3, 4)
>>> p1 is p2
False

Even though p1 and p2 contain the same coordinates, they are not the same object. If we assign p1 to p3, then the two variables are aliases of the same object:

>>> p3 = p1
>>> p1 is p3
True

This type of equality is called shallow equality because it compares only the references, not the contents of the objects.

To compare the contents of the objects — deep equality — we can write a function called same_coordinates:

def same_coordinates(p1, p2):
    return (p1.x == p2.x) and (p1.y == p2.y)

Now if we create two different objects that contain the same data, we can use same_point to find out if they represent points with the same coordinates.

>>> p1 = Point(3, 4)
>>> p2 = Point(3, 4)
>>> same_coordinates(p1, p2)
True

Of course, if the two variables refer to the same object, they have both shallow and deep equality.

Beware of ==

“When I use a word,” Humpty Dumpty said, in a rather scornful tone, “it means just what I choose it to mean — neither more nor less.” Alice in Wonderland

Python has a powerful feature that allows a designer of a class to decide what an operation like == or < should mean. (We’ve just shown how we can control how our own objects are converted to strings, so we’ve already made a start!) We’ll cover more detail later. But sometimes the implementors will attach shallow equality semantics, and sometimes deep equality, as shown in this little experiment:

p = Point(4, 2)
s = Point(4, 2)
print("== on Points returns", p == s)
# By default, == on Point objects does a shallow equality test

a = [2,3]
b = [2,3]
print("== on lists returns",  a == b)
# But by default, == does a deep equality test on lists

This outputs:

== on Points returns False
== on lists returns True

So we conclude that even though the two lists (or tuples, etc.) are distinct objects with different memory addresses, for lists the == operator tests for deep equality, while in the case of points it makes a shallow test.

Copying

Aliasing can make a program difficult to read because changes made in one place might have unexpected effects in another place. It is hard to keep track of all the variables that might refer to a given object.

Copying an object is often an alternative to aliasing. The copy module contains a function called copy that can duplicate any object:

>>> import copy
>>> p1 = Point(3, 4)
>>> p2 = copy.copy(p1)
>>> p1 is p2
False
>>> same_coordinates(p1, p2)
True

Once we import the copy module, we can use the copy function to make a new Point. p1 and p2 are not the same point, but they contain the same data.

To copy a simple object like a Point, which doesn’t contain any embedded objects, copy is sufficient. This is called shallow copying.

For something like a Rectangle, which contains a reference to a Point, copy doesn’t do quite the right thing. It copies the reference to the Point object, so both the old Rectangle and the new one refer to a single Point.

If we create a box, b1, in the usual way and then make a copy, b2, using copy, the resulting state diagram looks like this:

This is almost certainly not what we want. In this case, invoking grow on one of the Rectangle objects would not affect the other, but invoking move on either would affect both! This behavior is confusing and error-prone. The shallow copy has created an alias to the Point that represents the corner.

Fortunately, the copy module contains a function named deepcopy that copies not only the object but also any embedded objects. It won’t be surprising to learn that this operation is called a deep copy.

>>> b2 = copy.deepcopy(b1)

Now b1 and b2 are completely separate objects.

Glossary

deep copy

To copy the contents of an object as well as any embedded objects, and any objects embedded in them, and so on; implemented by the deepcopy function in the copy module.

deep equality

Equality of values, or two references that point to objects that have the same value.

shallow copy

To copy the contents of an object, including any references to embedded objects; implemented by the copy function in the copy module.

shallow equality

Equality of references, or two references that point to the same object.

Exercises

1. Add a method area to the Rectangle class that returns the area of any instance:

   r = Rectangle(Point(0, 0), 10, 5)
   test(r.area() == 50)
   

2. Write a perimeter method in the Rectangle class so that we can find the perimeter of any rectangle instance:

   r = Rectangle(Point(0, 0), 10, 5)
   test(r.perimeter() == 30)
   

3. Write a flip method in the Rectangle class that swaps the width and the height of any rectangle instance:

   r = Rectangle(Point(100, 50), 10, 5)
   test(r.width == 10 and r.height == 5)
   r.flip()
   test(r.width == 5 and r.height == 10)
   

4. Write a new method in the Rectangle class to test if a Point falls within the rectangle. For this exercise, assume that a rectangle at (0,0) with width 10 and height 5 has open upper bounds on the width and height, i.e. it stretches in the x direction from [0 to 10), where 0 is included but 10 is excluded, and from [0 to 5) in the y direction. So it does not contain the point (10, 2). These tests should pass:

   r = Rectangle(Point(0, 0), 10, 5)
   test(r.contains(Point(0, 0)))
   test(r.contains(Point(3, 3)))
   test(not r.contains(Point(3, 7)))
   test(not r.contains(Point(3, 5)))
   test(r.contains(Point(3, 4.99999)))
   test(not r.contains(Point(-3, -3)))
   

5. In games, we often put a rectangular “bounding box” around our sprites. (A sprite is an object that can move about in the game, as we will see shortly.) We can then do collision detection between, say, bombs and spaceships, by comparing whether their rectangles overlap anywhere.

   Write a function to determine whether two rectangles collide. Hint: this might be quite a tough exercise! Think carefully about all the cases before you code.

Even more OOP

MyTime

As another example of a user-defined type, we’ll define a class called MyTime that records the time of day. We’ll provide an __init__ method to ensure that every instance is created with appropriate attributes and initialization. The class definition looks like this:

class MyTime:

    def __init__(self, hrs=0, mins=0, secs=0):
        """ Create a MyTime object initialized to hrs, mins, secs """
        self.hours = hrs
        self.minutes = mins
        self.seconds = secs

We can instantiate a new MyTime object:

tim1 = MyTime(11, 59, 30)

The state diagram for the object looks like this:

We’ll leave it as an exercise for the readers to add a __str__ method so that MyTime objects can print themselves decently.

Pure functions

In the next few sections, we’ll write two versions of a function called add_time, which calculates the sum of two MyTime objects. They will demonstrate two kinds of functions: pure functions and modifiers.

The following is a rough version of add_time:

def add_time(t1, t2):
    h = t1.hours + t2.hours
    m = t1.minutes + t2.minutes
    s = t1.seconds + t2.seconds
    sum_t = MyTime(h, m, s)
    return sum_t

The function creates a new MyTime object and returns a reference to the new object. This is called a pure function because it does not modify any of the objects passed to it as parameters and it has no side effects, such as updating global variables, displaying a value, or getting user input.

Here is an example of how to use this function. We’ll create two MyTime objects: current_time, which contains the current time; and bread_time, which contains the amount of time it takes for a breadmaker to make bread. Then we’ll use add_time to figure out when the bread will be done.

>>> current_time = MyTime(9, 14, 30)
>>> bread_time = MyTime(3, 35, 0)
>>> done_time = add_time(current_time, bread_time)
>>> print(done_time)
12:49:30

The output of this program is 12:49:30, which is correct. On the other hand, there are cases where the result is not correct. Can you think of one?

The problem is that this function does not deal with cases where the number of seconds or minutes adds up to more than sixty. When that happens, we have to carry the extra seconds into the minutes column or the extra minutes into the hours column.

Here’s a better version of the function:

def add_time(t1, t2):

    h = t1.hours + t2.hours
    m = t1.minutes + t2.minutes
    s = t1.seconds + t2.seconds

    if s >= 60:
        s -= 60
        m += 1

    if m >= 60:
        m -= 60
        h += 1

    sum_t = MyTime(h, m, s)
    return sum_t

This function is starting to get bigger, and still doesn’t work for all possible cases. Later we will suggest an alternative approach that yields better code.

Modifiers

There are times when it is useful for a function to modify one or more of the objects it gets as parameters. Usually, the caller keeps a reference to the objects it passes, so any changes the function makes are visible to the caller. Functions that work this way are called modifiers.

increment, which adds a given number of seconds to a MyTime object, would be written most naturally as a modifier. A rough draft of the function looks like this:

def increment(t, secs):
    t.seconds += secs

    if t.seconds >= 60:
        t.seconds -= 60
        t.minutes += 1

    if t.minutes >= 60:
        t.minutes -= 60
        t.hours += 1

The first line performs the basic operation; the remainder deals with the special cases we saw before.

Is this function correct? What happens if the parameter seconds is much greater than sixty? In that case, it is not enough to carry once; we have to keep doing it until seconds is less than sixty. One solution is to replace the if statements with while statements:

def increment(t, seconds):
    t.seconds += seconds

    while t.seconds >= 60:
        t.seconds -= 60
        t.minutes += 1

    while t.minutes >= 60:
        t.minutes -= 60
        t.hours += 1

This function is now correct when seconds is not negative, and when hours does not exceed 23, but it is not a particularly good solution.

Converting increment to a method

Once again, OOP programmers would prefer to put functions that work with MyTime objects into the MyTime class, so let’s convert increment to a method. To save space, we will leave out previously defined methods, but you should keep them in your version:

class MyTime:
    # Previous method definitions here...

    def increment(self, seconds):
        self.seconds += seconds

        while self.seconds >= 60:
            self.seconds -= 60
            self.minutes += 1

        while self.minutes >= 60:
            self.minutes -= 60
            self.hours += 1

The transformation is purely mechanical — we move the definition into the class definition and (optionally) change the name of the first parameter to self, to fit with Python style conventions.

Now we can invoke increment using the syntax for invoking a method.

current_time.increment(500)

Again, the object on which the method is invoked gets assigned to the first parameter, self. The second parameter, seconds gets the value 500.

An “Aha!” insight

Often a high-level insight into the problem can make the programming much easier.

In this case, the insight is that a MyTime object is really a three-digit number in base 60! The second component is the ones column, the minute component is the sixties column, and the hour component is the thirty-six hundreds column.

When we wrote add_time and increment, we were effectively doing addition in base 60, which is why we had to carry from one column to the next.

This observation suggests another approach to the whole problem — we can convert a MyTime object into a single number and take advantage of the fact that the computer knows how to do arithmetic with numbers. The following method is added to the MyTime class to convert any instance into a corresponding number of seconds:

class MyTime:
    # ...

    def to_seconds(self):
        """ Return the number of seconds represented
            by this instance
        """
        return self.hours * 3600 + self.minutes * 60 + self.seconds

Now, all we need is a way to convert from an integer back to a MyTime object. Supposing we have tsecs seconds, some integer division and mod operators can do this for us:

hrs = tsecs // 3600
leftoversecs = tsecs % 3600
mins = leftoversecs // 60
secs = leftoversecs % 60

You might have to think a bit to convince yourself that this technique to convert from one base to another is correct.

In OOP we’re really trying to wrap together the data and the operations that apply to it. So we’d like to have this logic inside the MyTime class. A good solution is to rewrite the class initializer so that it can cope with initial values of seconds or minutes that are outside the normalized values. (A normalized time would be something like 3 hours 12 minutes and 20 seconds. The same time, but unnormalized could be 2 hours 70 minutes and 140 seconds.)

Let’s rewrite a more powerful initializer for MyTime:

class MyTime:
   # ...

   def __init__(self, hrs=0, mins=0, secs=0):
       """ Create a new MyTime object initialized to hrs, mins, secs.
           The values of mins and secs may be outside the range 0-59,
           but the resulting MyTime object will be normalized.
       """

       # Calculate total seconds to represent
       totalsecs = hrs*3600 + mins*60 + secs
       self.hours = totalsecs // 3600        # Split in h, m, s
       leftoversecs = totalsecs % 3600
       self.minutes = leftoversecs // 60
       self.seconds = leftoversecs % 60

Now we can rewrite add_time like this:

def add_time(t1, t2):
    secs = t1.to_seconds() + t2.to_seconds()
    return MyTime(0, 0, secs)

This version is much shorter than the original, and it is much easier to demonstrate or reason that it is correct.

Generalization

In some ways, converting from base 60 to base 10 and back is harder than just dealing with times. Base conversion is more abstract; our intuition for dealing with times is better.

But if we have the insight to treat times as base 60 numbers and make the investment of writing the conversions, we get a program that is shorter, easier to read and debug, and more reliable.

It is also easier to add features later. For example, imagine subtracting two MyTime objects to find the duration between them. The naive approach would be to implement subtraction with borrowing. Using the conversion functions would be easier and more likely to be correct.

Ironically, sometimes making a problem harder (or more general) makes the programming easier, because there are fewer special cases and fewer opportunities for error.

Specialization versus Generalization

Computer Scientists are generally fond of specializing their types, while mathematicians often take the opposite approach, and generalize everything.

What do we mean by this?

If we ask a mathematician to solve a problem involving weekdays, days of the century, playing cards, time, or dominoes, their most likely response is to observe that all these objects can be represented by integers. Playing cards, for example, can be numbered from 0 to 51. Days within the century can be numbered. Mathematicians will say “These things are enumerable — the elements can be uniquely numbered (and we can reverse this numbering to get back to the original concept). So let’s number them, and confine our thinking to integers. Luckily, we have powerful techniques and a good understanding of integers, and so our abstractions — the way we tackle and simplify these problems — is to try to reduce them to problems about integers.”

Computer Scientists tend to do the opposite. We will argue that there are many integer operations that are simply not meaningful for dominoes, or for days of the century. So we’ll often define new specialized types, like MyTime, because we can restrict, control, and specialize the operations that are possible. Object-oriented programming is particularly popular because it gives us a good way to bundle methods and specialized data into a new type.

Both approaches are powerful problem-solving techniques. Often it may help to try to think about the problem from both points of view — “What would happen if I tried to reduce everything to very few primitive types?”, versus “What would happen if this thing had its own specialized type?”

Another example

The after function should compare two times, and tell us whether the first time is strictly after the second, e.g.

>>> t1 = MyTime(10, 55, 12)
>>> t2 = MyTime(10, 48, 22)
>>> after(t1, t2)             # Is t1 after t2?
True

This is slightly more complicated because it operates on two MyTime objects, not just one. But we’d prefer to write it as a method anyway — in this case, a method on the first argument:

class MyTime:
    # Previous method definitions here...

    def after(self, time2):
        """ Return True if I am strictly greater than time2 """
        if self.hours > time2.hours:
            return True
        if self.hours < time2.hours:
            return False

        if self.minutes > time2.minutes:
            return True
        if self.minutes < time2.minutes:
            return False
        if self.seconds > time2.seconds:
            return True

        return False

We invoke this method on one object and pass the other as an argument:

if current_time.after(done_time):
    print("The bread will be done before it starts!")

We can almost read the invocation like English: If the current time is after the done time, then…

The logic of the if statements deserve special attention here. Lines 11-18 will only be reached if the two hour fields are the same. Similarly, the test at line 16 is only executed if both times have the same hours and the same minutes.

Could we make this easier by using our “Aha!” insight and extra work from earlier, and reducing both times to integers? Yes, with spectacular results!

class MyTime:
    # Previous method definitions here...

    def after(self, time2):
        """ Return True if I am strictly greater than time2 """
        return self.to_seconds() > time2.to_seconds()

This is a great way to code this: if we want to tell if the first time is after the second time, turn them both into integers and compare the integers.

Operator overloading

Some languages, including Python, make it possible to have different meanings for the same operator when applied to different types. For example, + in Python means quite different things for integers and for strings. This feature is called operator overloading.

It is especially useful when programmers can also overload the operators for their own user-defined types.

For example, to override the addition operator +, we can provide a method named __add__:

class MyTime:
    # Previously defined methods here...

    def __add__(self, other):
        return MyTime(0, 0, self.to_seconds() + other.to_seconds())

As usual, the first parameter is the object on which the method is invoked. The second parameter is conveniently named other to distinguish it from self. To add two MyTime objects, we create and return a new MyTime object that contains their sum.

Now, when we apply the + operator to MyTime objects, Python invokes the __add__ method that we have written:

>>> t1 = MyTime(1, 15, 42)
>>> t2 = MyTime(3, 50, 30)
>>> t3 = t1 + t2
>>> print(t3)
05:06:12

The expression t1 + t2 is equivalent to t1.__add__(t2), but obviously more elegant. As an exercise, add a method __sub__(self, other) that overloads the subtraction operator, and try it out.

For the next couple of exercises we’ll go back to the Point class defined in our first chapter about objects, and overload some of its operators. Firstly, adding two points adds their respective (x, y) coordinates:

class Point:
    # Previously defined methods here...

    def __add__(self, other):
        return Point(self.x + other.x,  self.y + other.y)

There are several ways to override the behavior of the multiplication operator: by defining a method named __mul__, or __rmul__, or both.

If the left operand of * is a Point, Python invokes __mul__, which assumes that the other operand is also a Point. It computes the dot product of the two Points, defined according to the rules of linear algebra:

def __mul__(self, other):
    return self.x * other.x + self.y * other.y

If the left operand of * is a primitive type and the right operand is a Point, Python invokes __rmul__, which performs scalar multiplication:

def __rmul__(self, other):
    return Point(other * self.x,  other * self.y)

The result is a new Point whose coordinates are a multiple of the original coordinates. If other is a type that cannot be multiplied by a floating-point number, then __rmul__ will yield an error.

This example demonstrates both kinds of multiplication:

>>> p1 = Point(3, 4)
>>> p2 = Point(5, 7)
>>> print(p1 * p2)
43
>>> print(2 * p2)
(10, 14)

What happens if we try to evaluate p2 * 2? Since the first parameter is a Point, Python invokes __mul__ with 2 as the second argument. Inside __mul__, the program tries to access the x coordinate of other, which fails because an integer has no attributes:

>>> print(p2 * 2)
AttributeError: 'int' object has no attribute 'x'

Unfortunately, the error message is a bit opaque. This example demonstrates some of the difficulties of object-oriented programming. Sometimes it is hard enough just to figure out what code is running.

Polymorphism

Most of the methods we have written only work for a specific type. When we create a new object, we write methods that operate on that type.

But there are certain operations that we will want to apply to many types, such as the arithmetic operations in the previous sections. If many types support the same set of operations, we can write functions that work on any of those types.

For example, the multadd operation (which is common in linear algebra) takes three parameters; it multiplies the first two and then adds the third. We can write it in Python like this:

def multadd (x, y, z):
    return x * y + z

This function will work for any values of x and y that can be multiplied and for any value of z that can be added to the product.

We can invoke it with numeric values:

>>> multadd (3, 2, 1)
7

Or with Points:

>>> p1 = Point(3, 4)
>>> p2 = Point(5, 7)
>>> print(multadd (2, p1, p2))
(11, 15)
>>> print(multadd (p1, p2, 1))
44

In the first case, the Point is multiplied by a scalar and then added to another Point. In the second case, the dot product yields a numeric value, so the third parameter also has to be a numeric value.

A function like this that can take arguments with different types is called polymorphic.

As another example, consider the function front_and_back, which prints a list twice, forward and backward:

def front_and_back(front):
    import copy
    back = copy.copy(front)
    back.reverse()
    print(str(front) + str(back))

Because the reverse method is a modifier, we make a copy of the list before reversing it. That way, this function doesn’t modify the list it gets as a parameter.

Here’s an example that applies front_and_back to a list:

>>> my_list = [1, 2, 3, 4]
>>> front_and_back(my_list)
[1, 2, 3, 4][4, 3, 2, 1]

Of course, we intended to apply this function to lists, so it is not surprising that it works. What would be surprising is if we could apply it to a Point.

To determine whether a function can be applied to a new type, we apply Python’s fundamental rule of polymorphism, called the duck typing rule: If all of the operations inside the function can be applied to the type, the function can be applied to the type. The operations in the front_and_back function include copy, reverse, and print.

Not all programming languages define polymorphism in this way. Look up duck typing, and see if you can figure out why it has this name.

copy works on any object, and we have already written a __str__ method for Point objects, so all we need is a reverse method in the Point class:

def reverse(self):
    (self.x , self.y) = (self.y, self.x)

Then we can pass Points to front_and_back:

>>> p = Point(3, 4)
>>> front_and_back(p)
(3, 4)(4, 3)

The most interesting polymorphism is the unintentional kind, where we discover that a function we have already written can be applied to a type for which we never planned.

Glossary

dot product

An operation defined in linear algebra that multiplies two Points and yields a numeric value.

functional programming style

A style of program design in which the majority of functions are pure.

modifier

A function or method that changes one or more of the objects it receives as parameters. Most modifier functions are void (do not return a value).

normalized

Data is said to be normalized if it fits into some reduced range or set of rules. We usually normalize our angles to values in the range [0..360). We normalize minutes and seconds to be values in the range [0..60). And we’d be surprised if the local store advertised its cold drinks at “One dollar, two hundred and fifty cents”.

operator overloading

Extending built-in operators ( +, -, *, >, <, etc.) so that they do different things for different types of arguments. We’ve seen early in the book how + is overloaded for numbers and strings, and here we’ve shown how to further overload it for user-defined types.

polymorphic

A function that can operate on more than one type. Notice the subtle distinction: overloading has different functions (all with the same name) for different types, whereas a polymorphic function is a single function that can work for a range of types.

pure function

A function that does not modify any of the objects it receives as parameters. Most pure functions are fruitful rather than void.

scalar multiplication

An operation defined in linear algebra that multiplies each of the coordinates of a Point by a numeric value.

Exercises

1. Write a Boolean function between that takes two MyTime objects, t1 and t2, as arguments, and returns True if the invoking object falls between the two times. Assume t1 <= t2, and make the test closed at the lower bound and open at the upper bound, i.e. return True if t1 <= obj < t2.

2. Turn the above function into a method in the MyTime class.

3. Overload the necessary operator(s) so that instead of having to write

   if t1.after(t2): ...
   

   we can use the more convenient

   if t1 > t2: ...
   

4. Rewrite increment as a method that uses our “Aha” insight.

5. Create some test cases for the increment method. Consider specifically the case where the number of seconds to add to the time is negative. Fix up increment so that it handles this case if it does not do so already. (You may assume that you will never subtract more seconds than are in the time object.)

6. Can physical time be negative, or must time always move in the forward direction? Some serious physicists think this is not such a dumb question. See what you can find on the Internet about this.

Collections of objects

Composition

By now, we have seen several examples of composition. One of the first examples was using a method invocation as part of an expression. Another example is the nested structure of statements; we can put an if statement within a while loop, within another if statement, and so on.

Having seen this pattern, and having learned about lists and objects, we should not be surprised to learn that we can create lists of objects. We can also create objects that contain lists (as attributes); we can create lists that contain lists; we can create objects that contain objects; and so on.

In this chapter and the next, we will look at some examples of these combinations, using Card objects as an example.

Card objects

If you are not familiar with common playing cards, now would be a good time to get a deck, or else this chapter might not make much sense. There are fifty-two cards in a deck, each of which belongs to one of four suits and one of thirteen ranks. The suits are Spades, Hearts, Diamonds, and Clubs (in descending order in bridge). The ranks are Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, and King. Depending on the game that we are playing, the rank of Ace may be higher than King or lower than 2. The rank is sometimes called the face-value of the card.

If we want to define a new object to represent a playing card, it is obvious what the attributes should be: rank and suit. It is not as obvious what type the attributes should be. One possibility is to use strings containing words like "Spade" for suits and "Queen" for ranks. One problem with this implementation is that it would not be easy to compare cards to see which had a higher rank or suit.

An alternative is to use integers to encode the ranks and suits. By encode, we do not mean what some people think, which is to encrypt or translate into a secret code. What a computer scientist means by encode is to define a mapping between a sequence of numbers and the items I want to represent. For example:

Spades   -->  3
Hearts   -->  2
Diamonds -->  1
Clubs    -->  0

An obvious feature of this mapping is that the suits map to integers in order, so we can compare suits by comparing integers. The mapping for ranks is fairly obvious; each of the numerical ranks maps to the corresponding integer, and for face cards:

Jack   -->  11
Queen  -->  12
King   -->  13

The reason we are using mathematical notation for these mappings is that they are not part of the Python program. They are part of the program design, but they never appear explicitly in the code. The class definition for the Card type looks like this:

class Card:
    def __init__(self, suit=0, rank=0):
        self.suit = suit
        self.rank = rank

As usual, we provide an initialization method that takes an optional parameter for each attribute.

To create some objects, representing say the 3 of Clubs and the Jack of Diamonds, use these commands:

three_of_clubs = Card(0, 3)
card1 = Card(1, 11)

In the first case above, for example, the first argument, 0, represents the suit Clubs.

Save this code for later use …

In the next chapter we assume that we have save the Cards class, and the upcoming Deck class in a file called Cards.py.

Class attributes and the __str__ method

In order to print Card objects in a way that people can easily read, we want to map the integer codes onto words. A natural way to do that is with lists of strings. We assign these lists to class attributes at the top of the class definition:

class Card:
    suits = ["Clubs", "Diamonds", "Hearts", "Spades"]
    ranks = ["narf", "Ace", "2", "3", "4", "5", "6", "7",
             "8", "9", "10", "Jack", "Queen", "King"]

    def __init__(self, suit=0, rank=0):
        self.suit = suit
        self.rank = rank

    def __str__(self):
        return (self.ranks[self.rank] + " of " + self.suits[self.suit])

A class attribute is defined outside of any method, and it can be accessed from any of the methods in the class.

Inside __str__, we can use suits and ranks to map the numerical values of suit and rank to strings. For example, the expression self.suits[self.suit] means use the attribute suit from the object self as an index into the class attribute named suits, and select the appropriate string.

The reason for the "narf" in the first element in ranks is to act as a place keeper for the zero-eth element of the list, which will never be used. The only valid ranks are 1 to 13. This wasted item is not entirely necessary. We could have started at 0, as usual, but it is less confusing to encode the rank 2 as integer 2, 3 as 3, and so on.

With the methods we have so far, we can create and print cards:

>>> card1 = Card(1, 11)
>>> print(card1)
Jack of Diamonds

Class attributes like suits are shared by all Card objects. The advantage of this is that we can use any Card object to access the class attributes:

>>> card2 = Card(1, 3)
>>> print(card2)
3 of Diamonds
>>> print(card2.suits[1])
Diamonds

Because every Card instance references the same class attribute, we have an aliasing situation. The disadvantage is that if we modify a class attribute, it affects every instance of the class. For example, if we decide that Jack of Diamonds should really be called Jack of Swirly Whales, we could do this:

>>> card1.suits[1] = "Swirly Whales"
>>> print(card1)
Jack of Swirly Whales

The problem is that all of the Diamonds just became Swirly Whales:

>>> print(card2)
3 of Swirly Whales

It is usually not a good idea to modify class attributes.

Comparing cards

For primitive types, there are six relational operators ( <, >, ==, etc.) that compare values and determine when one is greater than, less than, or equal to another. If we want our own types to be comparable using the syntax of these relational operators, we need to define six corresponding special methods in our class.

We’d like to start with a single method named cmp that houses the logic of ordering. By convention, a comparison method takes two parameters, self and other, and returns 1 if the first object is greater, -1 if the second object is greater, and 0 if they are equal to each other.

Some types are completely ordered, which means that we can compare any two elements and tell which is bigger. For example, the integers and the floating-point numbers are completely ordered. Some types are unordered, which means that there is no meaningful way to say that one element is bigger than another. For example, the fruits are unordered, which is why we cannot compare apples and oranges, and we cannot meaningfully order a collection of images, or a collection of cellphones.

Playing cards are partially ordered, which means that sometimes we can compare cards and sometimes not. For example, we know that the 3 of Clubs is higher than the 2 of Clubs, and the 3 of Diamonds is higher than the 3 of Clubs. But which is better, the 3 of Clubs or the 2 of Diamonds? One has a higher rank, but the other has a higher suit.

In order to make cards comparable, we have to decide which is more important, rank or suit. To be honest, the choice is arbitrary. For the sake of choosing, we will say that suit is more important, because a new deck of cards comes sorted with all the Clubs together, followed by all the Diamonds, and so on.

With that decided, we can write cmp:

def cmp(self, other):
    # Check the suits
    if self.suit > other.suit: return 1
    if self.suit < other.suit: return -1
    # Suits are the same... check ranks
    if self.rank > other.rank: return 1
    if self.rank < other.rank: return -1
    # Ranks are the same... it's a tie
    return 0

In this ordering, Aces appear lower than Deuces (2s).

Now, we can define the six special methods that do the overloading of each of the relational operators for us:

def __eq__(self, other):
    return self.cmp(other) == 0

def __le__(self, other):
    return self.cmp(other) <= 0

def __ge__(self, other):
    return self.cmp(other) >= 0

def __gt__(self, other):
    return self.cmp(other) > 0

def __lt__(self, other):
    return self.cmp(other) < 0

def __ne__(self, other):
    return self.cmp(other) != 0

With this machinery in place, the relational operators now work as we’d like them to:

>>> card1 = Card(1, 11)
>>> card2 = Card(1, 3)
>>> card3 = Card(1, 11)
>>> card1 < card2
False
>>> card1 == card3
True

Decks

Now that we have objects to represent Cards, the next logical step is to define a class to represent a Deck. Of course, a deck is made up of cards, so each Deck object will contain a list of cards as an attribute. Many card games will need at least two different decks — a red deck and a blue deck.

The following is a class definition for the Deck class. The initialization method creates the attribute cards and generates the standard pack of fifty-two cards:

class Deck:
    def __init__(self):
        self.cards = []
        for suit in range(4):
            for rank in range(1, 14):
                self.cards.append(Card(suit, rank))

The easiest way to populate the deck is with a nested loop. The outer loop enumerates the suits from 0 to 3. The inner loop enumerates the ranks from 1 to 13. Since the outer loop iterates four times, and the inner loop iterates thirteen times, the total number of times the body is executed is fifty-two (thirteen times four). Each iteration creates a new instance of Card with the current suit and rank, and appends that card to the cards list.

With this in place, we can instantiate some decks:

red_deck = Deck()
blue_deck = Deck()

Printing the deck

As usual, when we define a new type we want a method that prints the contents of an instance. To print a Deck, we traverse the list and print each Card:

class Deck:
    ...
    def print_deck(self):
        for card in self.cards:
            print(card)

Here, and from now on, the ellipsis (...) indicates that we have omitted the other methods in the class.

As an alternative to print_deck, we could write a __str__ method for the Deck class. The advantage of __str__ is that it is more flexible. Rather than just printing the contents of the object, it generates a string representation that other parts of the program can manipulate before printing, or store for later use.

Here is a version of __str__ that returns a string representation of a Deck. To add a bit of pizzazz, it arranges the cards in a cascade where each card is indented one space more than the previous card:

class Deck:
    ...
    def __str__(self):
        s = ""
        for i in range(len(self.cards)):
            s = s + " " * i + str(self.cards[i]) + "\n"
        return s

This example demonstrates several features. First, instead of traversing self.cards and assigning each card to a variable, we are using i as a loop variable and an index into the list of cards.

Second, we are using the string multiplication operator to indent each card by one more space than the last. The expression " " * i yields a number of spaces equal to the current value of i.

Third, instead of using the print command to print the cards, we use the str function. Passing an object as an argument to str is equivalent to invoking the __str__ method on the object.

Finally, we are using the variable s as an accumulator. Initially, s is the empty string. Each time through the loop, a new string is generated and concatenated with the old value of s to get the new value. When the loop ends, s contains the complete string representation of the Deck, which looks like this:

>>> red_deck = Deck()
>>> print(red_deck)
Ace of Clubs
 2 of Clubs
  3 of Clubs
   4 of Clubs
     5 of Clubs
       6 of Clubs
        7 of Clubs
         8 of Clubs
          9 of Clubs
           10 of Clubs
            Jack of Clubs
             Queen of Clubs
              King of Clubs
               Ace of Diamonds
                2 of Diamonds
                 ...

And so on. Even though the result appears on 52 lines, it is one long string that contains newlines.

Shuffling the deck

If a deck is perfectly shuffled, then any card is equally likely to appear anywhere in the deck, and any location in the deck is equally likely to contain any card.

To shuffle the deck, we will use the randrange function from the random module. With two integer arguments, a and b, randrange chooses a random integer in the range a <= x < b. Since the upper bound is strictly less than b, we can use the length of a list as the second parameter, and we are guaranteed to get a legal index. For example, if rng has already been instantiated as a random number source, this expression chooses the index of a random card in a deck:

rng.randrange(0, len(self.cards))

An easy way to shuffle the deck is by traversing the cards and swapping each card with a randomly chosen one. It is possible that the card will be swapped with itself, but that is fine. In fact, if we precluded that possibility, the order of the cards would be less than entirely random:

class Deck:
    ...
    def shuffle(self):
        import random
        rng = random.Random()        # Create a random generator
        num_cards = len(self.cards)
        for i in range(num_cards):
            j = rng.randrange(i, num_cards)
            (self.cards[i], self.cards[j]) = (self.cards[j], self.cards[i])

Rather than assume that there are fifty-two cards in the deck, we get the actual length of the list and store it in num_cards.

For each card in the deck, we choose a random card from among the cards that haven’t been shuffled yet. Then we swap the current card (i) with the selected card (j). To swap the cards we use a tuple assignment:

(self.cards[i], self.cards[j]) = (self.cards[j], self.cards[i])

While this is a good shuffling method, a random number generator object also has a shuffle method that can shuffle elements in a list, in place. So we could rewrite this function to use the one provided for us:

class Deck:
    ...
    def shuffle(self):
        import random
        rng = random.Random()        # Create a random generator
        rng.shuffle(self.cards)      # uUse its shuffle method

Removing and dealing cards

Another method that would be useful for the Deck class is remove, which takes a card as a parameter, removes it, and returns True if the card was in the deck and False otherwise:

class Deck:
    ...
    def remove(self, card):
        if card in self.cards:
            self.cards.remove(card)
            return True
        else:
            return False

The in operator returns True if the first operand is in the second. If the first operand is an object, Python uses the object’s __eq__ method to determine equality with items in the list. Since the __eq__ we provided in the Card class checks for deep equality, the remove method checks for deep equality.

To deal cards, we want to remove and return the top card. The list method pop provides a convenient way to do that:

class Deck:
    ...
    def pop(self):
        return self.cards.pop()

Actually, pop removes the last card in the list, so we are in effect dealing from the bottom of the deck.

One more operation that we are likely to want is the Boolean function is_empty, which returns True if the deck contains no cards:

class Deck:
    ...
    def is_empty(self):
        return self.cards == []

Glossary

encode

To represent one type of value using another type of value by constructing a mapping between them.

class attribute

A variable that is defined inside a class definition but outside any method. Class attributes are accessible from any method in the class and are shared by all instances of the class.

accumulator

A variable used in a loop to accumulate a series of values, such as by concatenating them onto a string or adding them to a running sum.

Exercises

1. Modify cmp so that Aces are ranked higher than Kings.

Inheritance

Inheritance

The language feature most often associated with object-oriented programming is inheritance. Inheritance is the ability to define a new class that is a modified version of an existing class.

The primary advantage of this feature is that you can add new methods to a class without modifying the existing class. It is called inheritance because the new class inherits all of the methods of the existing class. Extending this metaphor, the existing class is sometimes called the parent class. The new class may be called the child class or sometimes subclass.

Inheritance is a powerful feature. Some programs that would be complicated without inheritance can be written concisely and simply with it. Also, inheritance can facilitate code reuse, since you can customize the behavior of parent classes without having to modify them. In some cases, the inheritance structure reflects the natural structure of the problem, which makes the program easier to understand.

On the other hand, inheritance can make programs difficult to read. When a method is invoked, it is sometimes not clear where to find its definition. The relevant code may be scattered among several modules. Also, many of the things that can be done using inheritance can be done as elegantly (or more so) without it. If the natural structure of the problem does not lend itself to inheritance, this style of programming can do more harm than good.

In this chapter we will demonstrate the use of inheritance as part of a program that plays the card game Old Maid. One of our goals is to write code that could be reused to implement other card games.

A hand of cards

For almost any card game, we need to represent a hand of cards. A hand is similar to a deck, of course. Both are made up of a set of cards, and both require operations like adding and removing cards. Also, we might like the ability to shuffle both decks and hands.

A hand is also different from a deck. Depending on the game being played, we might want to perform some operations on hands that don’t make sense for a deck. For example, in poker we might classify a hand (straight, flush, etc.) or compare it with another hand. In bridge, we might want to compute a score for a hand in order to make a bid.

This situation suggests the use of inheritance. If Hand is a subclass of Deck, it will have all the methods of Deck, and new methods can be added.

We add the code in this chapter to our Cards.py file from the previous chapter. In the class definition, the name of the parent class appears in parentheses:

class Hand(Deck):
    pass

This statement indicates that the new Hand class inherits from the existing Deck class.

The Hand constructor initializes the attributes for the hand, which are name and cards. The string name identifies this hand, probably by the name of the player that holds it. The name is an optional parameter with the empty string as a default value. cards is the list of cards in the hand, initialized to the empty list:

class Hand(Deck):
    def __init__(self, name=""):
       self.cards = []
       self.name = name

For just about any card game, it is necessary to add and remove cards from the deck. Removing cards is already taken care of, since Hand inherits remove from Deck. But we have to write add:

class Hand(Deck):
    ...
    def add(self, card):
        self.cards.append(card)

Again, the ellipsis indicates that we have omitted other methods. The list append method adds the new card to the end of the list of cards.

Dealing cards

Now that we have a Hand class, we want to deal cards from the Deck into hands. It is not immediately obvious whether this method should go in the Hand class or in the Deck class, but since it operates on a single deck and (possibly) several hands, it is more natural to put it in Deck.

deal should be fairly general, since different games will have different requirements. We may want to deal out the entire deck at once or add one card to each hand.

deal takes two parameters, a list (or tuple) of hands and the total number of cards to deal. If there are not enough cards in the deck, the method deals out all of the cards and stops:

class Deck:
    ...
    def deal(self, hands, num_cards=999):
        num_hands = len(hands)
        for i in range(num_cards):
            if self.is_empty():
                break                    # Break if out of cards
            card = self.pop()            # Take the top card
            hand = hands[i % num_hands]  # Whose turn is next?
            hand.add(card)               # Add the card to the hand

The second parameter, num_cards, is optional; the default is a large number, which effectively means that all of the cards in the deck will get dealt.

The loop variable i goes from 0 to num_cards-1. Each time through the loop, a card is removed from the deck using the list method pop, which removes and returns the last item in the list.

The modulus operator (%) allows us to deal cards in a round robin (one card at a time to each hand). When i is equal to the number of hands in the list, the expression i % num_hands wraps around to the beginning of the list (index 0).

Printing a Hand

To print the contents of a hand, we can take advantage of the __str__ method inherited from Deck. For example:

>>> deck = Deck()
>>> deck.shuffle()
>>> hand = Hand("frank")
>>> deck.deal([hand], 5)
>>> print(hand)
Hand frank contains
2 of Spades
 3 of Spades
  4 of Spades
   Ace of Hearts
    9 of Clubs

It’s not a great hand, but it has the makings of a straight flush.

Although it is convenient to inherit the existing methods, there is additional information in a Hand object we might want to include when we print one. To do that, we can provide a __str__ method in the Hand class that overrides the one in the Deck class:

class Hand(Deck)
    ...
    def __str__(self):
        s = "Hand " + self.name
        if self.is_empty():
            s += " is empty\n"
        else:
            s += " contains\n"
        return s + Deck.__str__(self)

Initially, s is a string that identifies the hand. If the hand is empty, the program appends the words is empty and returns s.

Otherwise, the program appends the word contains and the string representation of the Deck, computed by invoking the __str__ method in the Deck class on self.

It may seem odd to send self, which refers to the current Hand, to a Deck method, until you remember that a Hand is a kind of Deck. Hand objects can do everything Deck objects can, so it is legal to send a Hand to a Deck method.

In general, it is always legal to use an instance of a subclass in place of an instance of a parent class.

The CardGame class

The CardGame class takes care of some basic chores common to all games, such as creating the deck and shuffling it:

class CardGame:
    def __init__(self):
        self.deck = Deck()
        self.deck.shuffle()

This is the first case we have seen where the initialization method performs a significant computation, beyond initializing attributes.

To implement specific games, we can inherit from CardGame and add features for the new game. As an example, we’ll write a simulation of Old Maid.

The object of Old Maid is to get rid of cards in your hand. You do this by matching cards by rank and color. For example, the 4 of Clubs matches the 4 of Spades since both suits are black. The Jack of Hearts matches the Jack of Diamonds since both are red.

To begin the game, the Queen of Clubs is removed from the deck so that the Queen of Spades has no match. The fifty-one remaining cards are dealt to the players in a round robin. After the deal, all players match and discard as many cards as possible.

When no more matches can be made, play begins. In turn, each player picks a card (without looking) from the closest neighbor to the left who still has cards. If the chosen card matches a card in the player’s hand, the pair is removed. Otherwise, the card is added to the player’s hand. Eventually all possible matches are made, leaving only the Queen of Spades in the loser’s hand.

In our computer simulation of the game, the computer plays all hands. Unfortunately, some nuances of the real game are lost. In a real game, the player with the Old Maid goes to some effort to get their neighbor to pick that card, by displaying it a little more prominently, or perhaps failing to display it more prominently, or even failing to fail to display that card more prominently. The computer simply picks a neighbor’s card at random.

OldMaidHand class

A hand for playing Old Maid requires some abilities beyond the general abilities of a Hand. We will define a new class, OldMaidHand, that inherits from Hand and provides an additional method called remove_matches:

class OldMaidHand(Hand):
    def remove_matches(self):
        count = 0
        original_cards = self.cards[:]
        for card in original_cards:
            match = Card(3 - card.suit, card.rank)
            if match in self.cards:
                self.cards.remove(card)
                self.cards.remove(match)
                print("Hand {0}: {1} matches {2}"
                        .format(self.name, card, match))
                count += 1
        return count

We start by making a copy of the list of cards, so that we can traverse the copy while removing cards from the original. Since self.cards is modified in the loop, we don’t want to use it to control the traversal. Python can get quite confused if it is traversing a list that is changing!

For each card in the hand, we figure out what the matching card is and go looking for it. The match card has the same rank and the other suit of the same color. The expression 3 - card.suit turns a Club (suit 0) into a Spade (suit 3) and a Diamond (suit 1) into a Heart (suit 2). You should satisfy yourself that the opposite operations also work. If the match card is also in the hand, both cards are removed.

The following example demonstrates how to use remove_matches:

>>> game = CardGame()
>>> hand = OldMaidHand("frank")
>>> game.deck.deal([hand], 13)
>>> print(hand)
Hand frank contains
Ace of Spades
 2 of Diamonds
  7 of Spades
   8 of Clubs
    6 of Hearts
     8 of Spades
      7 of Clubs
       Queen of Clubs
        7 of Diamonds
         5 of Clubs
          Jack of Diamonds
           10 of Diamonds
            10 of Hearts
>>> hand.remove_matches()
Hand frank: 7 of Spades matches 7 of Clubs
Hand frank: 8 of Spades matches 8 of Clubs
Hand frank: 10 of Diamonds matches 10 of Hearts
>>> print(hand)
Hand frank contains
Ace of Spades
 2 of Diamonds
  6 of Hearts
   Queen of Clubs
    7 of Diamonds
     5 of Clubs
      Jack of Diamonds

Notice that there is no __init__ method for the OldMaidHand class. We inherit it from Hand.

OldMaidGame class

Now we can turn our attention to the game itself. OldMaidGame is a subclass of CardGame with a new method called play that takes a list of players as a parameter.

Since __init__ is inherited from CardGame, a new OldMaidGame object contains a new shuffled deck:

class OldMaidGame(CardGame):
    def play(self, names):
        # Remove Queen of Clubs
        self.deck.remove(Card(0,12))

        # Make a hand for each player
        self.hands = []
        for name in names:
            self.hands.append(OldMaidHand(name))

        # Deal the cards
        self.deck.deal(self.hands)
        print("---------- Cards have been dealt")
        self.print_hands()

        # Remove initial matches
        matches = self.remove_all_matches()
        print("---------- Matches discarded, play begins")
        self.print_hands()

        # Play until all 50 cards are matched
        turn = 0
        num_hands = len(self.hands)
        while matches < 25:
            matches += self.play_one_turn(turn)
            turn = (turn + 1) % num_hands

        print("---------- Game is Over")
        self.print_hands()

The writing of print_hands has been left as an exercise.

Some of the steps of the game have been separated into methods. remove_all_matches traverses the list of hands and invokes remove_matches on each:

class OldMaidGame(CardGame):
    ...
    def remove_all_matches(self):
        count = 0
        for hand in self.hands:
            count += hand.remove_matches()
        return count

count is an accumulator that adds up the number of matches in each hand. When we’ve gone through every hand, the total is returned (count).

When the total number of matches reaches twenty-five, fifty cards have been removed from the hands, which means that only one card is left and the game is over.

The variable turn keeps track of which player’s turn it is. It starts at 0 and increases by one each time; when it reaches num_hands, the modulus operator wraps it back around to 0.

The method play_one_turn takes a parameter that indicates whose turn it is. The return value is the number of matches made during this turn:

class OldMaidGame(CardGame):
    ...
    def play_one_turn(self, i):
        if self.hands[i].is_empty():
            return 0
        neighbor = self.find_neighbor(i)
        picked_card = self.hands[neighbor].pop()
        self.hands[i].add(picked_card)
        print("Hand", self.hands[i].name, "picked", picked_card)
        count = self.hands[i].remove_matches()
        self.hands[i].shuffle()
        return count

If a player’s hand is empty, that player is out of the game, so he or she does nothing and returns 0.

Otherwise, a turn consists of finding the first player on the left that has cards, taking one card from the neighbor, and checking for matches. Before returning, the cards in the hand are shuffled so that the next player’s choice is random.

The method find_neighbor starts with the player to the immediate left and continues around the circle until it finds a player that still has cards:

class OldMaidGame(CardGame):
    ...
    def find_neighbor(self, i):
        num_hands = len(self.hands)
        for next in range(1,num_hands):
            neighbor = (i + next) % num_hands
            if not self.hands[neighbor].is_empty():
                return neighbor

If find_neighbor ever went all the way around the circle without finding cards, it would return None and cause an error elsewhere in the program. Fortunately, we can prove that that will never happen (as long as the end of the game is detected correctly).

We have omitted the print_hands method. You can write that one yourself.

The following output is from a truncated form of the game where only the top fifteen cards (tens and higher) were dealt to three players. With this small deck, play stops after seven matches instead of twenty-five.

>>> import cards
>>> game = cards.OldMaidGame()
>>> game.play(["Allen","Jeff","Chris"])
---------- Cards have been dealt
Hand Allen contains
King of Hearts
 Jack of Clubs
  Queen of Spades
   King of Spades
    10 of Diamonds

Hand Jeff contains
Queen of Hearts
 Jack of Spades
  Jack of Hearts
   King of Diamonds
    Queen of Diamonds

Hand Chris contains
Jack of Diamonds
 King of Clubs
  10 of Spades
   10 of Hearts
    10 of Clubs

Hand Jeff: Queen of Hearts matches Queen of Diamonds
Hand Chris: 10 of Spades matches 10 of Clubs
---------- Matches discarded, play begins
Hand Allen contains
King of Hearts
 Jack of Clubs
  Queen of Spades
   King of Spades
    10 of Diamonds

Hand Jeff contains
Jack of Spades
 Jack of Hearts
  King of Diamonds

Hand Chris contains
Jack of Diamonds
 King of Clubs
  10 of Hearts

Hand Allen picked King of Diamonds
Hand Allen: King of Hearts matches King of Diamonds
Hand Jeff picked 10 of Hearts
Hand Chris picked Jack of Clubs
Hand Allen picked Jack of Hearts
Hand Jeff picked Jack of Diamonds
Hand Chris picked Queen of Spades
Hand Allen picked Jack of Diamonds
Hand Allen: Jack of Hearts matches Jack of Diamonds
Hand Jeff picked King of Clubs
Hand Chris picked King of Spades
Hand Allen picked 10 of Hearts
Hand Allen: 10 of Diamonds matches 10 of Hearts
Hand Jeff picked Queen of Spades
Hand Chris picked Jack of Spades
Hand Chris: Jack of Clubs matches Jack of Spades
Hand Jeff picked King of Spades
Hand Jeff: King of Clubs matches King of Spades
---------- Game is Over
Hand Allen is empty

Hand Jeff contains
Queen of Spades

Hand Chris is empty

So Jeff loses.

Glossary

inheritance

The ability to define a new class that is a modified version of a previously defined class.

parent class

The class from which a child class inherits.

child class

A new class created by inheriting from an existing class; also called a subclass.

Exercises

1. Add a method, print_hands, to the OldMaidGame class which traverses self.hands and prints each hand.
2. Define a new kind of Turtle, TurtleGTX, that comes with some extra features: it can jump forward a given distance, and it has an odometer that keeps track of how far the turtle has travelled since it came off the production line. (The parent class has a number of synonyms like fd, forward, back, backward, and bk: for this exercise, just focus on putting this functionality into the forward method.) Think carefully about how to count the distance if the turtle is asked to move forward by a negative amount. (We would not want to buy a second-hand turtle whose odometer reading was faked because its previous owner drove it backwards around the block too often. Try this in a car near you, and see if the car’s odometer counts up or down when you reverse.)
3. After travelling some random distance, your turtle should break down with a flat tyre. After this happens, raise an exception whenever forward is called. Also provide a change_tyre method that can fix the flat.